高等数学下

第八章 向量代数与空间解析几何

第一节 向量及其线性运算

沿（x/y/z）方向余弦值：坐标值/模长
Prja（下标）b：b在a方向上的投影
（其余的东西都是高中学过的，不做赘述）

第二节 向量积、数量积、混合积

 向量积：a·b=|a||b| cosθ
 数量积：a×b=|a||b| sinθ/行列式D的值（其中第一行为i，j，k，第二第三行为a、b的坐标）
 混合积：（a×b）·c的值为行列式D的值（其中一到三行分别为a，b，c的坐标值）

第三节 平面及其方程

 平面方程求法：点法式
 已知平面的法向量n=（A，B，C）->n=AB×AC；有一点为（x0，y0，z0）；
 则平面方程为A(x-x0)+B(y-y0)+C(z-z0)=0;

第四节 空间直线及其方程

 空间直线求法：对称式（也叫点向式）及其参数方程
 已知直线的一点（x0，y0，z0）；直线的方向向量s=（A，B，C）->n1×n2,即两平面交线的方向向量为二者法向量叉乘；
 则(x-x0)/A=(y-y0)/B=(z-z0)/C;
 待定系数法求平面束：(ax+by+cz)+λ(Ax+By+Cz)=0

第五节 曲面及其方程

 椭球面：X^2/a^2+Y^2/b^2+Z^2/c^2=R^2 (当且仅当a=b=c时为球面)
 锥面：Z^2=X^2/a^2+Y^2/b^2   (当且仅当a=b时为圆锥面)
 抛物面：X^2+Y^2+Z=R^2
 单叶双曲面：X^2/a^2+Y^2/b^2-Z^2/c^2=1  （双曲线绕谁转谁不变）
 双叶双曲面：X^2/a^2-Y^2/b^2-Z^2/c^2=1  （双曲线绕谁转谁不变）
 椭圆/双曲抛物面：X^2/a^2+Y^2/b^2=Z  /   X^2/a^2-Y^2/b^2=Z
 柱面：一般没有那个字母母线就平行于哪个轴

第六节 空间曲线及其方程

 投影求法：若都有z，则先消去z，再联立z=0，找到封顶和封底。
 若没有z，则先把z=0代入有z的方程，观察是否切到另一平面的底面

空间曲线的参数方程：
X=a cos w t；Y=a sin w t；Z=v t ->螺旋上升成一个圆柱

第九章 多元函数微分法及其应用

第一节 多元函数的基本概念

一些新定义的点

 内点：在x-o-y平面中趋近于一点的邻域内的点叫内点
 外点：在x-o-y平面中趋近于一点的邻域外的点叫外点
 边界点：在x-o-y平面中趋近于一点的邻域上的点叫边界点
 E指的是边界点的全体，内点一定属于E，外点一定不属于E，边界点都有可能。
 聚点：任意一个点P，去心邻域中总有E中的点，则称P为E的聚点

平面点集

 开集：点集E的点都是E的内点
 闭集：点集E的边界点都属于E
 连通集：点集E中任意两点联通的折线属于E
 区域：连通的开集
 闭区域：联通的闭集
 有界集/无界集：顾名思义

极限

极限的定义：
和一元函数一样，二元函数的极限就是在x-o-y平面内从各个方向逼近于一个点的值
极限的求法：
和一元函数一样，需要用到有理化、代入、等价无穷小等方法。
连续的定义：l i m(x ,y)->(x0,y0)f(x, y)=f(x0,y0)；
证明极限不存在：
因为是二维平面，所以要证明极限时要从多个方向逼近。证明只用它的值会变。

练习例题

 1.	L i m(x->+∞, y->+∞)(x^2+y^2)*e^-(x^2+y^2)  (洛必达法则)
 2.	L i m(x->0,y->0)x y/(x^2+y^2)^1/2    (夹逼定理)
 3.	Lim(x ,y)->(0,0)(x^2+y^2)^1/2+sin(x^2+y^2)^1/2/(x^2+y^2)^3/2 (泰勒展开或洛必达)
 （sin x =x-1/3! X^2+0(u^3)）
 4.	Lim(x ,y)->(0,0)sin(x^2y)/(x^2+y^2)      (基本不等式)

练习题：（证明在（0，0）极限不存在）

 1.	f（x）=x y/(x^2+y^2),x^2+y^2≠0；0,x^2+y^2=0;  (切记要利用偏导的定义，定一求一 )
 2.	l i m(x ,y)->(0,0) x^2y/(x^4+y^2)  (选好一个方向趋近于（0，0）点)
 3.  l i m(x ,y)->(0,0) (1+xy)^1/(x+y)

第二节 偏导数

定义：沿着某个方向的斜率，定一求一，把另一个自变量当成常数进行求导
偏导≠>连续
若函数连续，则∂^2 z/∂x∂y=∂^2 z/∂y∂x

练习：

 1.	f(x ,y)=x+(y-1) arc sin(x/y)^1/2,求f x(x,1)
 2.	设函数u=f(r)二阶可导，且满足方程∂^2u/∂x^2+∂^2u/∂y^2=4,其中r=（x^2+y^2）^1/2,求f(r)

第三节 全微分

 偏增量：f(x+Δx ,y)-f(x ,y) / f(x ,y+Δy)-f(x ,y)
 偏微分: f x(x ,y)Δx/ f y(x ,y)Δy，其中Δx=d x，Δy=d y
 全增量：Δz=f(x+Δx ,y+Δy)-f(x ,y)=Ax +By+ρ(0); ρ(0)=(x^2+y^2)^1/2
 全微分：d z=f x(x ,y)Δx/ f y(x ,y)Δy

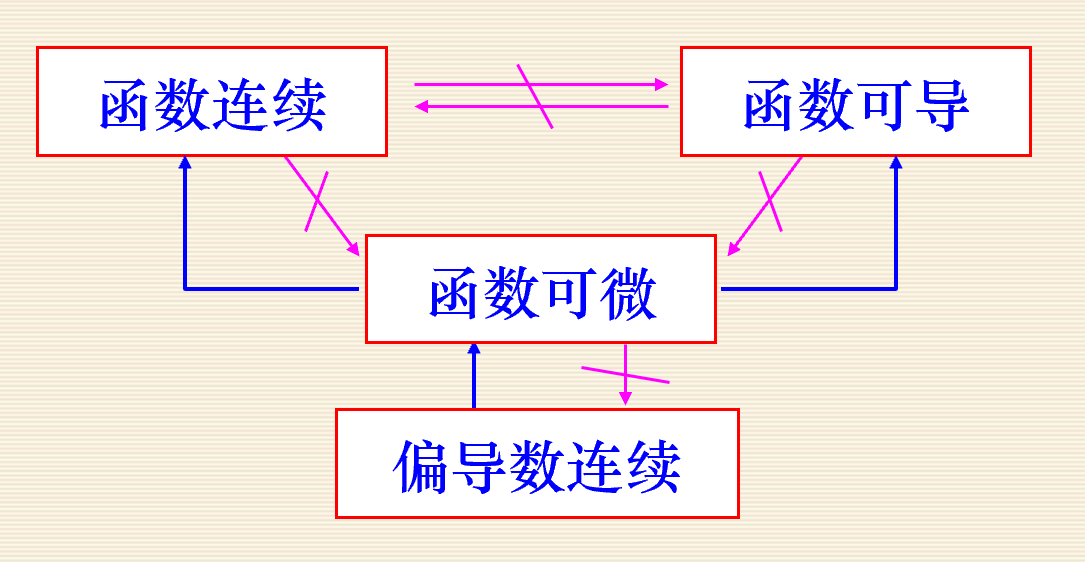
可微->连续/偏导存在
这是因为, 如果z=f(x, y)在点(x, y)可微, 则Δz=f(x+Δx, y+Δy)-f(x, y) =AΔx+BΔy+o(r),
于是lim（ρ→0）Δz=0，则l i m(Δx , Δy)->(0,0) f(x+Δx,y+Δy)=lim(ρ->0)[f(x,y)+Δz]=f(x,y)
偏导存在且连续->可微 （二者缺一不可）



求近似值的方法：
设定一个函数并且给x 、y赋值；再利用Δz≈d z=f x(x ,y)Δx+ f y(x ,y)Δy求出Δz；最后利用原式=z(x ,y)+Δz算出近似值

第四节 多元复合函数的求导法则

一元函数和多元函数符合求导

定义：若有z(u,v),u(t),v(t),求dz/dt （一元函数再多都一样）
∂z先对它自己的一个变量求偏导，再对那一个变量进行求偏导。
则有链式法则:dz/dt = ∂z/∂u * du/dt + ∂z/∂v * dv/dt; dz/dt 称为全导数；
证明：先利用连续的定义把Δz展开成：Δz = ∂z/∂u * Δu + ∂z/∂v * Δv。
然后再两边同时除dt得到结论。

多元函数和多元函数复合

定义：若有z=f(x,y),u(x,y),v(x,y),求若有z(u,v),u(t),v(t),求∂z/∂x和∂z/∂y
∂z先对它自己的一个变量求偏导，再对那一个变量进行求偏导。
则有链式法则：∂z/∂x = ∂z/∂u * ∂u/∂x + ∂z/∂v * ∂v/∂x;
∂z/∂y = ∂z/∂u * ∂u/∂y + ∂z/∂v * ∂v/∂y;
例题：
1.u=f(x.y.z)=e^(x^2+y^2+z^2),z=x^2siny,求∂z/∂x;∂z/∂y
2.(☆这里求二阶导很重要)设w=f(x+y+z,xyz)，f具有二阶偏导数，求∂w/∂x，∂^2w/∂x∂y
3.u=x-2y ,v=x+ay ,且方程 6∂^2z/∂x^2 - ∂^2z/∂y^2 + ∂^2z/∂x∂y=0可以简化为∂^2z/∂u∂v =0,求常数a；
4.设z=f(2x+3y,x^2y)+g(xy^2)，求∂^2z/∂x∂y;
答案：
1.
2.3.
3.
4.3.

第五节 隐函数的求导

一个方程的情形

隐函数存在定理1：
设函数在点的某一邻域内具有连续的偏导数，且F(x_0,y_0)=0,F_y(x_0,y_0)≠0,则方程F(x_0,y_0)=0在点(x_0,y_0)的某一邻域内恒能唯一确定一个单值连续且具有连续导数的函数y=f(x)，它满足条件y_0=f(x_0)，并有dy/dx=-（F_x/F_y）
隐函数存在定理2：
设函数在点的某一邻域内具有连续的偏导数，且F(x_0,y_0,z_0)=0,F_z(x_0,y_0,z_0)≠0,则方程F(x_0,y_0,z_0)=0在点(x_0,y_0,z_0)的某一邻域内恒能唯一确定一个单值连续且具有连续导数的函数z=f(x,y)，它满足条件z_0=f(x_0,y_0)，并有∂z/∂x=-(Fx/Fz);∂z/∂y=-(Fy/Fz).

方程组的情形

由方程组可以确定隐函数组（谁是谁的函数），利用克拉默法则->雅可比行列式，系数矩阵的行列式的值不能为0，因为会由无穷多解。
步骤：
若为对一个变量求导：(问什么导就求什么导)
先两边同时对分母那个自变量求导(复合函数求导)，然后利用克拉默法则求出答案
若为对两个变量求导：(问什么导就求什么导)
1.先两边同时对分母那个自变量求导(复合函数求导)，然后利用克拉默法则求出答案。->直接法
2.若u（x,y）,v(x,y),则求导数的话要用雅可比行列式，分母为F、G关于u、v的导数，分子就是求啥替换啥。->公式法

练习

设F（u，v）有连续偏导数，证明由方程F（x+z/y，y+z/x）所确定的函数z=（x，y）满足x ∂z/∂x+y ∂z/∂y=z-xy

第六节 ☆多元函数微分学的几何应用（与梯度下降有关）

空间曲线的切线与法平面

1.如果是参数方程，则x、y、z分别对参数求导求出切线的方向向量，然后可以通过点向式求切线，通过点法式求法平面
2.若不是参数方程，则将x/y/z作为参数进行计算

空间曲线的切平面

面在点处的法向量为对x、y、z分别求偏导的结果
TO BE CONTINUE……∂