离散数学

第一章 数理逻辑

第一节 绪论、命题

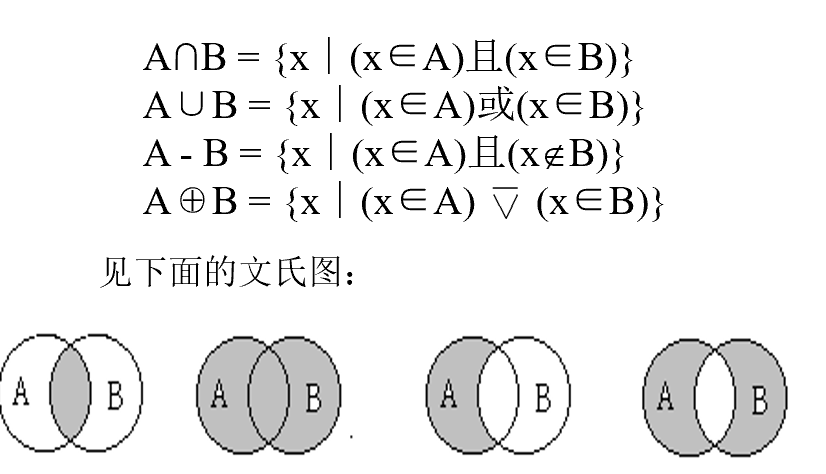
命题：不受时间限制，客观上能够确定真假的陈述句。

分类：

原子命题：不能分解为更简单的陈述句。
复合命题：由联结词、标点符号和原子命题复合构成的命题。
命题常量：用来表示确定命题的标识符。 例如：P表示“今天下雨。”
命题变元：表示任意命题位置标志的命题标识符。例如：P∨┑P， P∧Q。
指派：用一个特定命题取代命题变元P称为对P指派。

联结词：（越往上越优先）

  ┑：否定
 ∧：合取            全真才真，一假即假
 ∨：（可兼）析取     全假才假，一真即真。不可兼析取为 (P∧┑Q)∨(┑P∧Q)。
 ->：条件          只有真的推出假的才算假
 <->：双条件       当且仅当

练习题：

用A表示你走，用B表示我留下。
1.当你走，我将留下。
2.当且仅当你走，我将留下。
3.仅当你走我将留下。

第二节 真值表、重言式

命题公式：

单个命题变元或常元本身是一个命题公式；

真值表：

在命题公式中，对于分量指派真值的各种可能组合，就确定了这个命题公式的各种真值情况，把它汇列成表。

变元取值的顺序：（记结论）

☆按二进制递增或递减。n个命题变元组成的命题公式共有2^n种真值情况。
☆由n个命愿变元组成不等价的命题公式的个数为:2^2^n;

逻辑等价：两个命题公式A和B，对于任意一组真值指派， A和B的真值都相同，则称A和B是逻辑等价的或等价的。A<=>B

☆命题的定律：

       结合率  A∧(B∧C)<=>(A∧B)∧C
               A∨(B∨C)<=>(A∨B)∨C
       分配律  A∧(B∨C)<=>(A∧B)∨(A∧C)  
               A∨(B∧C)<=>(A∨B)∧(A∨C)
       德摩根律 ┑(A∨B)<=>┑A∧┑B
               ┑(A∧B)<=>┑A∨┑B
       ☆蕴含等值式 A->B<=>┑A∨B
       其他:P<->Q<=>（P∧Q）∨（┑P∧┑Q）  P<-> Q<=>（P→Q）∧（Q→P ）
       重言式、永真式   P∨┑P=1
       矛盾式、永假式   P∧┑P=0

例题：

1.	判断  ┑P∧（P∨Q）→q的真值
2.	验证（P∨Q）→r  <=>（P→r）∧（Q→r ）

第三节 蕴含式、其他联结词

蕴含式

定义：
当仅当P->Q是一个重言式时，我们称“ P 蕴含 Q ”，并记作 P=>Q(Q比P大)
证明方法：（一般用第一种,第四节会提及）

1、假设前提为真，往证结论为真；
2、假设结论为假，往证前提为假，即反证法

性质：

1.蕴含关系可传递
2.两个蕴含式结论的合并：A=>B，A=>C，得到A=>B∧C；
3.两个蕴含式前提的合并: B=>A，C=>A，得到B∨C=>A;

其他联结词

V上面加一杠为不可兼析取
↑与非  P↑Q <=> ┑(P∧Q)
↓或非  P↓Q <=> ┑(P∨Q)

最小联结词组

冗余联结词：
在一个联结词的集合中，如果一个联结词可以由集合中的其他联结词定义，否则称为独立联结词。
最小联结词组：
既能表示任意真值函数（不少），又不含冗余联结词（不多）的联结词集合称为最小联结词组（极小全功能集）。
☆以下联结词集合是最小联结词组：

第四节 对偶与范式

对偶式

定义：
在给定的命题公式A中，将联结词∧换成∨，∨换成∧，特殊变元 F 和 T 互换，所得公式A* 称为A的对偶式。
定理：

1.设A和A*是对偶式，P1,P2,…,Pn 是出现在A和A*中的原子变元，则
┑A(P1,P2,…,Pn) <=>A*(┑P1, ┑P2,…, ┑Pn)
A (┑P1, ┑P2,…, ┑Pn) <=> ┑ A* (P1,P2,…,Pn)
2.设P1,P2,…,Pn 是所有出现在命题公式A和B中的原子变元，如果A<=>B，则A*<=>B*。
3.A<=>T 当仅当  A*<=>F  

☆利用对偶式求命题的非：（定理一）

1.消去其他逻辑运算符，只留下┑、∧、∨（↑、↓）
2.用括号表示优先级
3.把 A 变为 A*  (∧∨互换、F T互换、↓↑互换)
4.所有变元Pi用┓Pi代入，得到┓A

例题：

A=>B,则A*=>B*正确吗

范式

定义：

1.合取范式：形式为A1∧A2∧……∧An的命题公式，其中Ai为命题变元或其否定所组成的析取式。例：(┑P∨Q)∧R∧(┑Q∨┑R) 
2.析取范式：形式为A1∨A2∨……∨An的命题公式，其中Ai为命题变元或其否定所组成的合取式。例：┑A∨┑B∨(A∧B) 
3.主析取(合取)范式：对于给定的命题公式，一个仅由最小(大)项的析取(合取)所组成的等价公式，称为该命题公式的主析(合取)取范式。

定理：在真值表中，一个公式的真值为T(F)的指派所对应的最小(大)项的析取(合取)，即为该公式的主析取(合取)范式。

例题：
1.求(p->q)<->r的合取范式与析取范式,主析取范式与主析取范式

最大项 最小项

1.(最)小项：n个命题变元的合取式，每个变元或其否定必需有一个且只有一个出现。例如：(A∧┑B)、(┑P∧Q∧R) 
2.(最)大项：n个命题变元的析取式，每个变元或其否定必需有一个且只有一个出现。
例如：(A∨┑B)、(┑P∨Q∨R) 
☆（结论）n个命题变元共有几个最大(小)项？ 分别有2^n个最大项和最小项

第五节 演绎与命题函数

演绎：

定义：
设S是一个命题公式的集合(前提集合)。从S推出公式G的一个演绎是公式的一个有限序列：G1, G2, …, Gk。其中，Gi或者是S，或者是某些 Gj(j< i)的逻辑结果。并且 Gk就是G。我们称公式G为此演绎的逻辑结果，或称从S演绎出G。有时也记为S=>G。
证明：

若给出前提集合S=【G1 ，…，Gk】，公式G，证明S=>G有如下两种方法：
1.G1∧ …∧ Gk =>G 
2. 形式演绎法

形式演绎法：

根据一些基本等价式和基本蕴涵式，从S出发，演绎出G。
在演绎过程中遵循以下三条规则：

P规则: 可随便使用前提。（抄前提）
T规则:可随便使用前面演绎出的某些公式的逻辑结果。 （抄自己的结果）
CP规则: 如果需要演绎出的公式是P->Q的形式，则我们可将P做为附加前提使用，而力图去演绎出Q。

练习题

1.证明【(P∨Q)，(P->R)，(Q->S)】=>S∨R
2.【P->(Q->S),┑R∨P,Q】=>R->S
3.A,B,C,D四人参加考试后，有人问它们，谁的成绩最好。A说“不是我”，B说“是D”，C说“是 B”，D说“不是我”。四人的回答只有一人符合实际，问是谁的成绩最好?只有一人成绩最好的是谁?(反证法推矛盾)
4.【R->┑Q,R∨S,S->┑Q,P->Q】=>┑P（两种方法）
5.【A->(b->C),(C∧D)->E,┑F->(D∧┑E)】=>A->(B->F)

谓词

定义：可以独立存在的物体叫个体，用于刻划个体的性质或关系的叫谓词
表示法：用大写字母表示谓词，用小写字母表示个体。
一元谓词表达了个体的性质；多元谓词表达了多个个体之间的关系。
例如：A表示“是大学生”； B表示“小于”。a表示“张山”；A(a)表示张山是大学生；B(b,c)表示“b小于c”；B(c,b)表示“c小于b”

谓词公式的等价

两个谓词公式A和B，若它们有共同的个体域E，且对A和B的任意一组变元进行赋值，所得的命题真值相同，则称谓词公式A和B在E上是等价的，记作A<=>B
谓词公式与个体域的关系：

谓词公式A在个体域E上的所有赋值都为真，则称谓词公式A在E上是有效的（永真的）
谓词公式A在个体域E上的所有赋值都为假，则称谓词公式A在E上是不可满足的（永假的）
谓词公式A在个体域E上的至少有一组赋值为真，则称谓词公式A在E上是可满足的

谓词填式

定义：谓词字母后面填上客体所得的式子叫谓词填式。
谓词与命题的关系：单独一个谓词不是完整命题，完整的客体和谓词字母两部分才成为一个命题。

命题函数

简单命题函数：
由一个谓词，一些客体变元组成的表达式称为简单命题函数。例如 A(x)、B(x,y)
复合命题函数：
由一个或多个命题函数以及逻辑联结词组合而成的表达式称为复合命题函数。例如 ┑A(x)、A(x)->┑B(x,y)

谓词与命题函数的关系：
n元谓词是n个客体变量的命题函数，命题函数不是命题，当客体变元取特定值时，命题函数才构成命题；命题是0元谓词；

量词

全称量词∀x，对所有的 x 
存在量词∃x，存在一些 x

二者在翻译时的区别：

M(x)表示x是人，H(x)表示x要呼吸
有些人要呼吸：(∃x)(M(x)∧H(x))
所有人要呼吸：(∀x)(M(x)->H(x))

谓词翻译与个体域

如果没有给定个体域，则要引入特性谓词
例如：所有正实数均可开平方。

R(x)：表示x是实数；
G(x)：表示x是正数；
B(x,y)：表示x大于y；
S(x)：表示x可开平方。
当个体域是正实数时：∀xS(x)
当个体域是实数时：∀x(G(x)∀S(x))或： ∀x(B(x,0)->S(x))
当个体域是全体时： ∀x(R(x)∧B(x,0)->S(x))

练习题：

用P(x)表示x来上课，用Q(y)表示y是好学生,请用带量词的谓词公式表示以下句子:
(1)来上课的学生都是好学生:
(2)不来上课的学生都不是好学生:
(3)并不是所有好学生都来上课:
(4)好学生不一定都来上课:
(5)所有的好学生都来上课:

答案：

(1)(∀x)(P(x)→Q(x))
(2)(∀x)(¬P(X) →¬Q(x))
(3) ¬((∃x)Q(x)->P(x))
(4)(∃x)(Q(x)∧P(x))
(5)(∀x)(Q(x)→p(x))

第六节 变元的约束，谓词的等价式与蕴含式

变元的辖域

量词后面紧跟的变元在谓词公式中起作用的范围，叫该变元的辖域（或叫作用域）
约束变元：
被量词修饰的变元称为约束变元，约束变元在作用域中的每次出现叫约束出现
自由变元：
没被量词修饰的变元称为自由变元，自由变元在谓词公式中的出现叫自由出现

约束变元的讨论：

n元谓词P(x1,x2,…,xn)具有 n 个相互独立的自由变元，若对其中的 k 个变元进行约束，则成为 (n-k) 元谓词。若谓词公式中没有自由变元，则谓词公式成为一个命题。
(∃x)(∀y)P(x,y,z)是一元谓词
(∃y)P(x,y,z)是二元谓词

约束变元的换名：

(∀x)P(x)与(∀y)P(y)意义相同，故可对约束变元进行换名；

有限域中消去量词

若x的个体域是有限集【a1,a2,…,an】，则有：

(∃x)A(x) <=> A(a1)∧A(a2)∧…∧A(an)
(∀x)A(x) <=> A(a1)∨A(a2)∨…∨A(an)

量词的不同出现顺序有不同的意义：(∃x)(∀y)P(x,y)不同于(∀y)(∃x)P(x,y)

☆量词与”┑”的关系

☆☆☆ ┑∀<=>∃┑ ;┑∃<=>∀┑

☆量词作用域的变化

在谓词公式中，可以将不含约束变元的命题任意移至量词的作用域之内或之外。

(∀x)(A(X)∧B(X)) <=> (∀x) A(X)∧(∀x) B(X)
(∃x)(A(X)∨B(X)) <=> (∃x) A(X)∨(∃x) B(X)
区分：
(∃x)(A(X)∧B(X)) => (∃x) A(X)∧(∃x) B(X)
(∀x) A(X)∨(∀x) B(X) =>(∀x) (A(X)∨B(X))

练习

1.用L(x,y)表示x喜欢y，用P(a)表示a是人，B(a)表示a是书，请用带量词的谓词公式表示以下句子:
(1)每个人都有自己喜欢的一本书:
(2)所有人都喜欢某本书:
2.论域是质数集，B(x,y)表示x比y大。表示“不存在最大的质数”的谓词公式是:

答案

1.
(1)(∀x)(P(x)->(∃y)(B(y)∧L(x,y)))
(2)(∃y)(B(y)∧((∀x)(P(x)->L(x,y))))
2.
┑((∃x)(∀yB(x,y)))

第七节 前束范式

定义：
一个谓词公式，如果量词都在整个式子的前头，其作用域延伸到整个谓词公式的末尾，这样的谓词公式叫前束范式。
定理：
任意一个谓词公式，都有一个与之等价的前束范式。

转化的步骤：

1.取消多余的量词
2.换名
3.消去条件、双条件联结词
4.将┑ 深入
5.将量词移至左边

练习：

1.把公式(∀x)(P(x))→(ヨx)Q(x)转化为前束范式。
2.化公式(∀x)(∀y)(((ヨz)P(x,z)∧P(y,z)))->(ヨu)(Q(x,y,u))化为前束范式
3.设I是如下一个解释：  D=【2,3】
F(2)  F(3)  P(2)  P(3)  Q(2,2)  Q(2,3)  Q(3,2)  Q(3,3)
3     2       0    1      1        1      0       1
求∀xヨy（P(x)∧Q（F（x），y））的真值。
4.证明：ヨx(F(x)->G(x)) <=> ∀yF(y) ->ヨzG(z)
5.L(x,y)表示y是x的先驱数，H(x,y)表示y是x的后继数，F(x)表示x是自然数，请用带量词的谓词公式表示以下句子：
1）有的自然数无先驱数：
2） 每个自然数都有后继数：
6.(∀x)(ヨy)(P(x)∧Q(y))   ------->谁靠近就先化简谁

答案

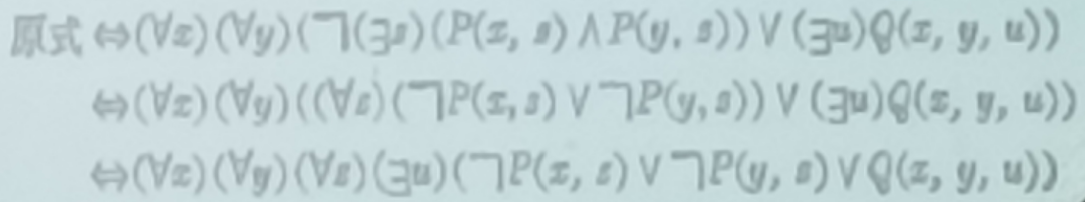
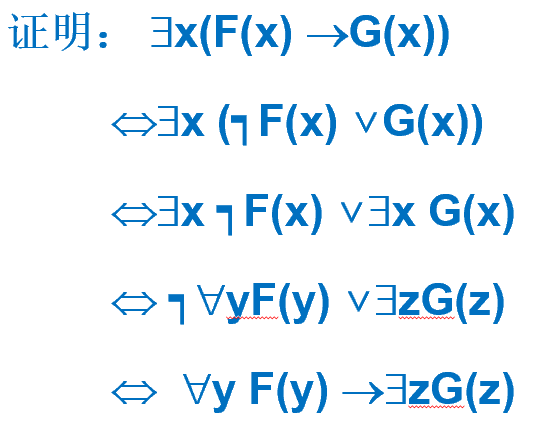
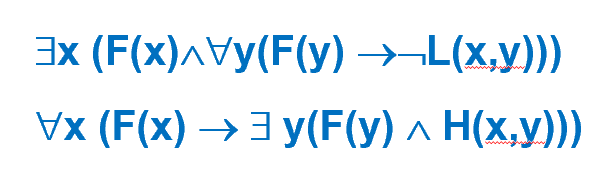
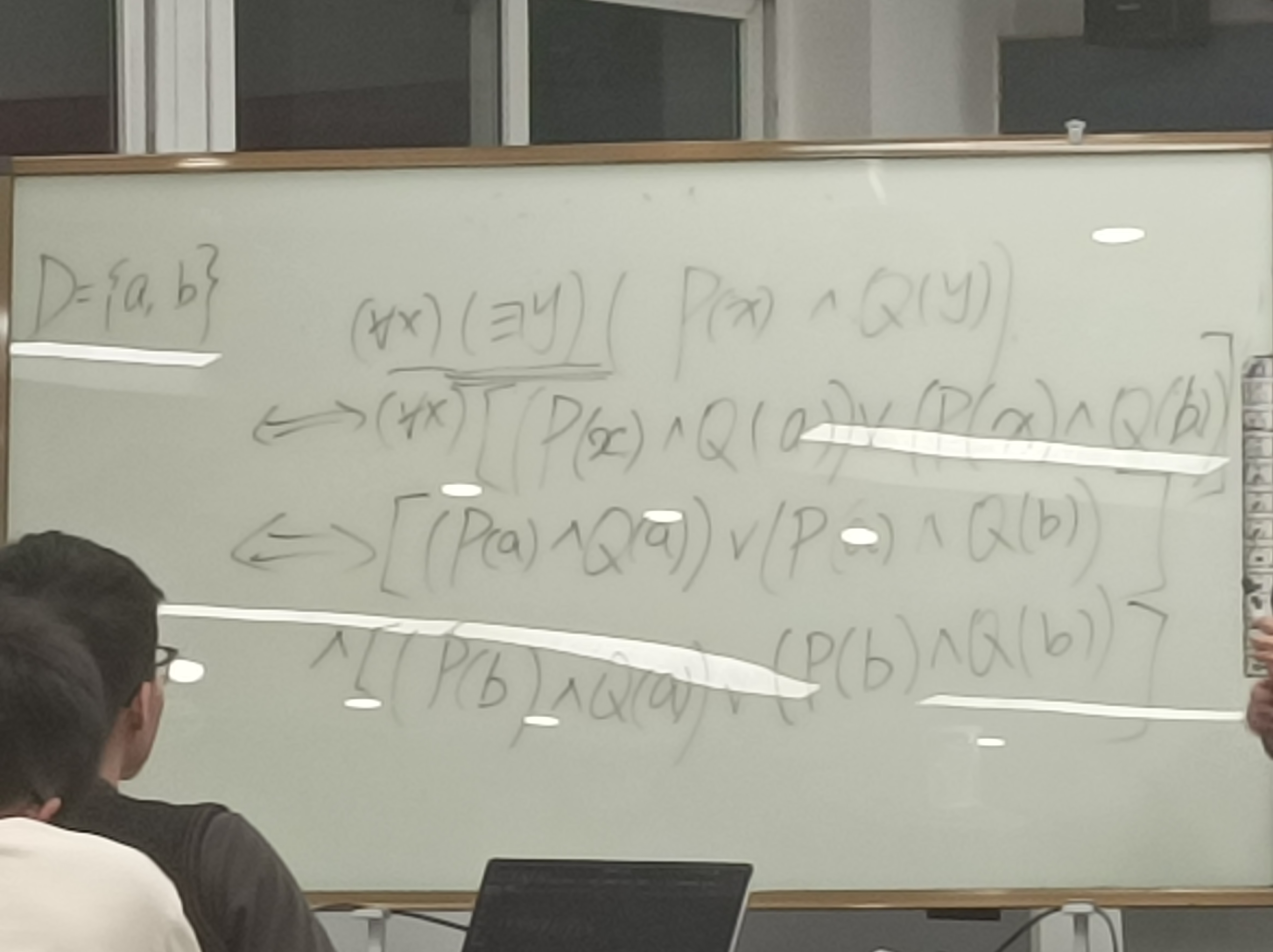
第二章 集合论

第一节 集合的运算

定义：集合是不能精确定义的基本概念，一般用大写字母表示集合，用小写字母表示元素。
集合与元素的关系：x∈A 或 x∉A
集合元素可以是离散型数据（如整型、逻辑型、枚举型等），也可以是非离散型数据（如实型）。有限集一定是离散型数据，无限集可能是离散型，也可能是非离散型的数据。本书中默认：自然数集从0开始
简单过一遍概念：



空集的性质：

1.空集是一切集合的子集。
2.空集是惟一的。
3.空集是任何集合的幂集的元素。
4.空集的幂集不是空集。

☆φ⊆【φ】；φ∈【φ】

幂集

定义：给定集合A，由集合A的所有子集为元素组成的集合，称为集合A的幂集。

补集

~A=E-A

集合运算的性质：

E = ~φ= A∪E = A∪~A 
φ= ~E = A∩φ=A∩~A= A⊕A = A - A
A = A∩A = A∩E= A∪A = A∪φ= A⊕φ= ~ (~A)
交换律和结合律只有减法不满足，其他的都可以
注意：A - B ≠ B - A /(A - B) - C ≠ A - ( B - C) 
☆分配律：
A∩(B∪C) = (A∩B)∪(A∩C)
A∪(B∩C) = (A∪B)∩(A∪C)
A∩(B - C)= (A∩B) - (A∩C)  
A∩(B⊕C) = ( A∩B)⊕(A∩C)
但不能：A∪(B - C ) ≠ (A∪B) - (A∪C)  
但：A∪(B⊕C) ≠ (A∪B)⊕(A∪C)
摩根律：
~ (A∪B) =  ~A∩ ~B 
~ (A∩B) =  ~A∪ ~B
吸收律：
A∪(A∩B) = A = A∩(A∪B)
其他：
A∩B ⊆A ⊆ A∪B
A∩B ⊆ B ⊆ A∪B
交集的补集=补集的交集
☆☆☆A - B = A∩ ~B = A - (A∩B)

练习（期末会有证明相等证明，一般会利用性质证明的方法多）

1.证明A=B，当且仅当A⊕B=φ。（双向证明）
2.已知ABC是集合，而且A⊕B=A⊕C，是否一定有B=C （两边同时⊕A，利用结合律做）
3.写出P（【a，【a】】）和P（【【1，【2，3】】】）的所有集合
4.若A⊆B，判断A的幂集是否⊆B的幂集。（∀x∈A，x∈B）
5.任意集合AB，A的幂集交B的幂集是否等于A交B的幂集（即证明P（A∩B）=P（A）∩P（B））
6.A的幂集-B的幂集是否等于A-B的幂集（任意举例）
7.证明对于任意集合ABC，有（A-B）-C=A-（B∪C）    （用好那个特别重要的式子）
8.已知A⊆B，证明：（B-A）∪A=B    （用好那个特别重要的式子）

第二节 包含排斥原理 序偶与笛卡儿乘积

包含排斥原理

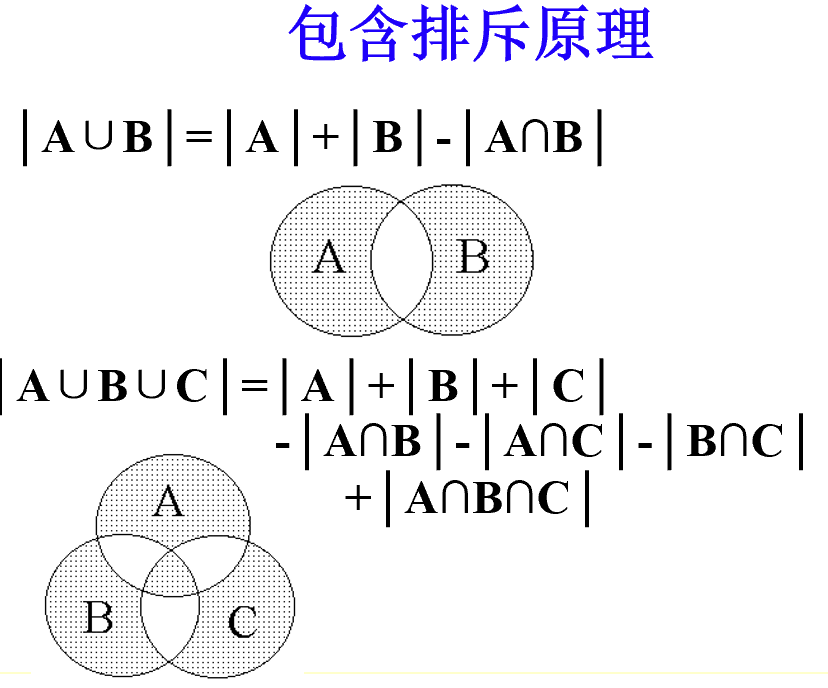
练习

1.某学校举行运动会，有短跑、跳高、跳远三项，二年级有180人，已知有25人三个项目都参加，参加两个项目以上的有85人，全年级参加比赛总人次为250人次。问有多少人没有参加任何项目?
2.12名小朋友，8人玩过山车，7人玩旋转木马，5人玩摩天轮，5人玩过山车和旋转木马，4人玩过山车和玩摩天轮，5人旋转木马和玩摩天轮。问：有多少人三种都没玩？
3.90名学生，55人参加数学小组,44人参加语文小组，33人参加体育小组，36人参加数学和语文小组，29人参加数学和体育小组，25人参加语文和体育小组。问:至少有多少人3个小组都没参加?

答案

1.
2.
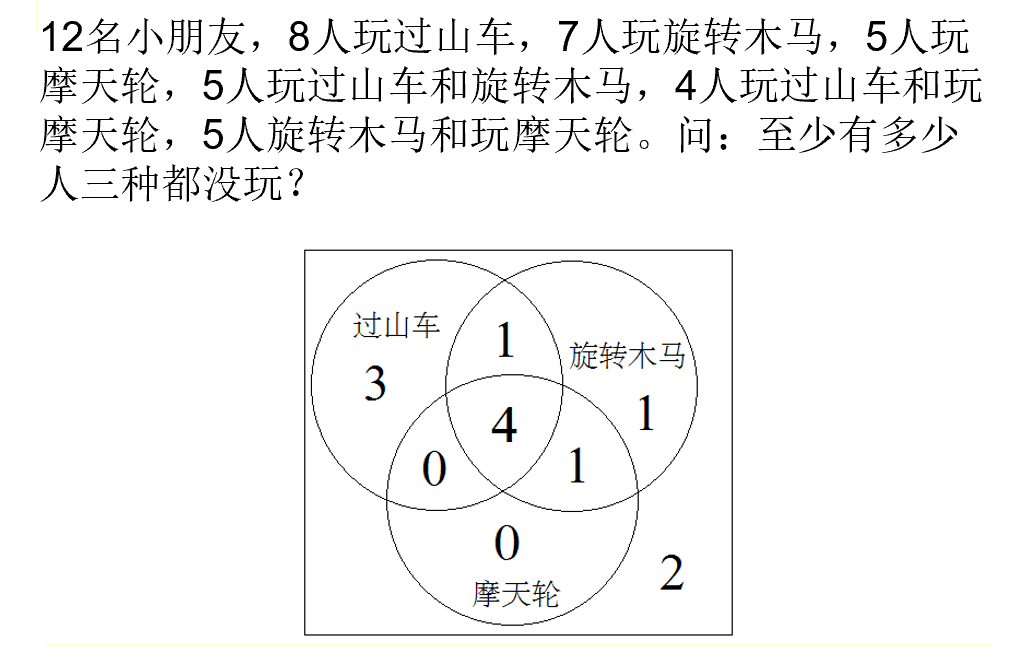
3.23人

序偶

有序的偶对。
若x≠y，则<x,y>≠<y,x>，但[x,y]=[y,x]
序偶与集合的统一：<x,y> = [[x],[x,y]]
序偶相等的定义：<x,y>=<u,v> <=> x=u 且 y=v
序偶的推广： < x , y , z > = <<x,y>, z >称为三元组.注意：<<x,y>, z >≠ <x, <y,z>>

笛卡尔乘积

公式：A×B = 【<x,y>|(x∈A)∧(y∈B)】（【】为大括号，因为直接打大括号系统会出错）
一些性质：

下面这个定理不常用，了解即可

练习：

1.若A×B=空集，则A=空集或B=空集；
2.A×A=B×B则A=B；（需要讨论A是否为空集）
3.ABCD为集合，则（A∩B）×（C∩D）=（A∩C）×（B∩D）

##### 答案：

1.若AB都不是空集，则存在x∈A，y∈B使A×B（x，y），与题目矛盾
2.①若A为非空集；任意x∈A，<x,x>∈A×A，<x,x>∈B×B，所以x∈B，A为B的子集，同理B为A的子集。
②若A为空集：则B×B为空集，则B为空集A=B

关系

定义：关系是两个集合的笛卡尔乘积的子集。
关系R是序偶的集合：若<x,y>∈R则记为xRy，反之记为xRy（在R上加一杠或者划掉R）
集合A到集合B的关系：A×B的子集。集合A上的关系：A×A的子集；

关系的域

关系R的前域: domR=[x|(存在y)(<x,y>∈R)]（大括号）—>所有的第一分量的集合
关系R的值域:ranR=[y|(存在x)(<x,y>∈R)]（大括号）—>所有的第二份量的集合
若R为AxB的子集，则domR⊆A 且ranR⊆B —>前域和值域求并集
关系的域 FLD R= domR U ranR
因为R ⊆ AxB ⊆ (AUB) x (AUB)，所以A到B的关系是(AUB)上的关系

练习

1.设X=[1,2,3,4],求X上的关系>及dom>,ran>.
2.x=[1,2,3,~~~~~,m]求大于关系和大于等于关系的元素
3.若|A|=m,|B|=n,|A×B|=?,A到B有多少个不同的关系(即A×B有多少个子集)，A上有多少不同的关系（即A×B有多少个子集）

答案

1.>=[<2,1>,<3,1><4,1><3,2>,<4,2>,<4,3>],剩下两个略
2.Cm2；Cm2+m
3.m*n；2^mn;2^m^2

特殊的关系

IA=[<x,x>|x∈A]是A上的关系
全域关系：R=A×B 
空关系：R=空集
定义：A到B的两个关系的交兵差不仍然是A到B的关系

关系的表示

1.集合法（枚举表示法）：列举集合的所有元素（序偶）
2.集合法（叙述法）：叙述关系定义的判别条件
3.矩阵法：A到B的关系用A行B列的0、1矩阵表示
4.图：A到B的关系：用有向偶图表示（点表示集合元素，弧表示序偶）
      A上的关系:用有向偶图表示（点表示集合元素，弧表示序偶）

练习

1.R[<1,1>,<2,2>]的补集
2.（嵌套序偶）令S=[1,2,3,4],A=SxS,在A上有关系R:<a,b>R<c,d>，当且仅当a+d=b+c,R?

答案

1.R的补集为[<1,2>,<2,1>]
2.

关系的性质（A上的关系）

讨论非空集合A上的关系R（即R⊆A×A）

自反性和反自反性（互斥）

自反性：(∀a∈A, <a,a >∈R；)
关系图中每个点都有环关系;矩阵是对角线元素全部为1;
反自反性：(∀a∈A, <a,a>∉R)
关系图中每个点都没环；关系矩阵是对角线元素全部为0;

对称性和反对称性（有交集，也可以都没有）

对称性： (∀a, b ∈A, 若<a,b>∈R，则<b,a>∈R)
关系图中任意两个不同的点之间要么没有边，要么有双向边；关系矩阵是对称矩阵
反对称性：(若a≠b，则<a,b>∉R或<b,a>∉R ；或者：∀a,b∈A, 若<a,b>∈R且<b,a>∈R, 则a=b；)

传递性

∀ a,b,c∈A, 若 <a,b>∈R 且 <b,c>∈R，则<a,c>∈R
关系图中任意两个点之间若经过第三点有路接通，则必有直达边;关系矩阵较复杂

☆例子：

注意第一个图和第二个图的第二个式子的对比，说明了若有<1,2>和<2,1>互指，则传递出<1,1>,即必须要有环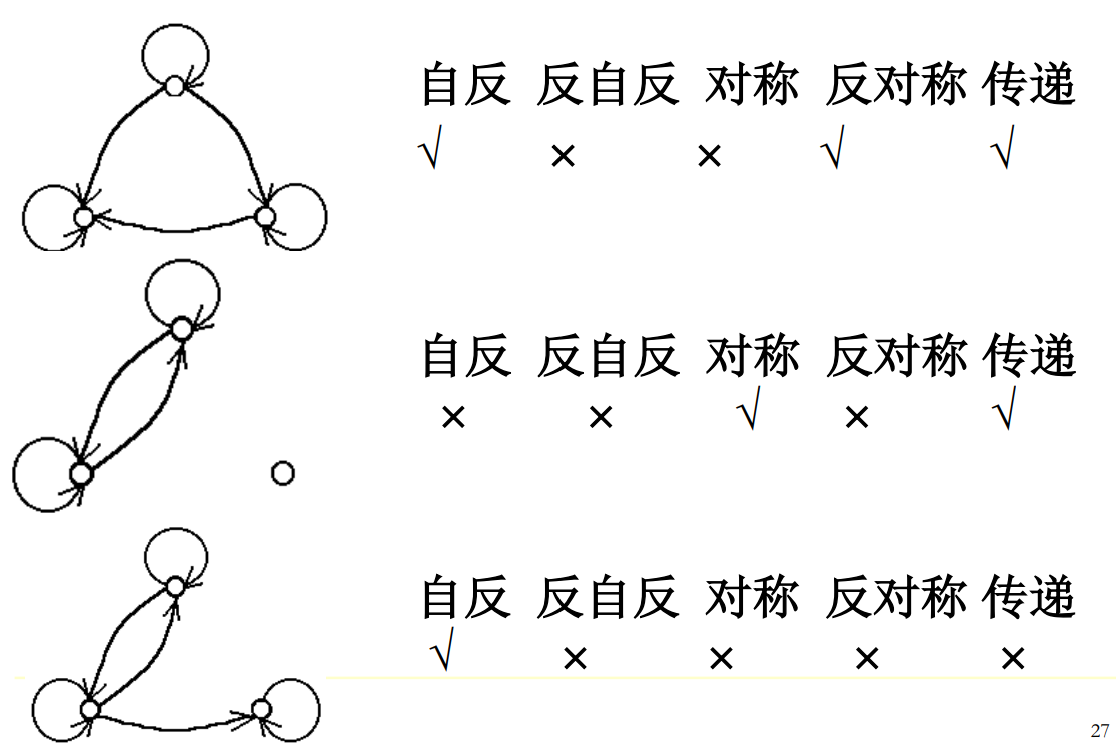




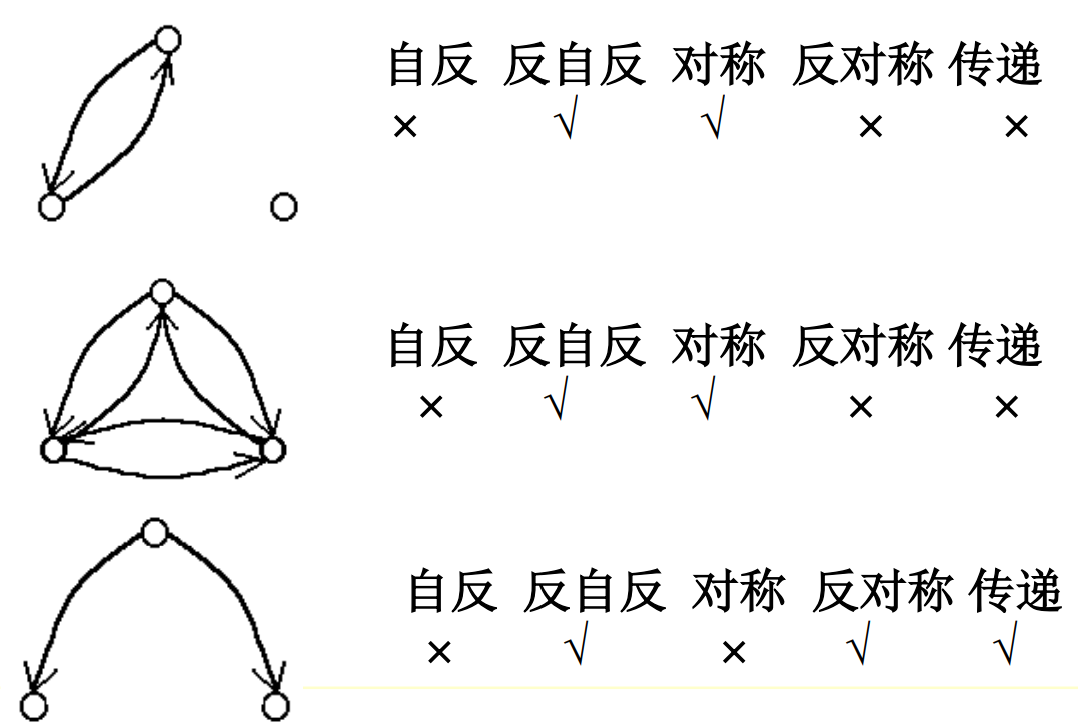
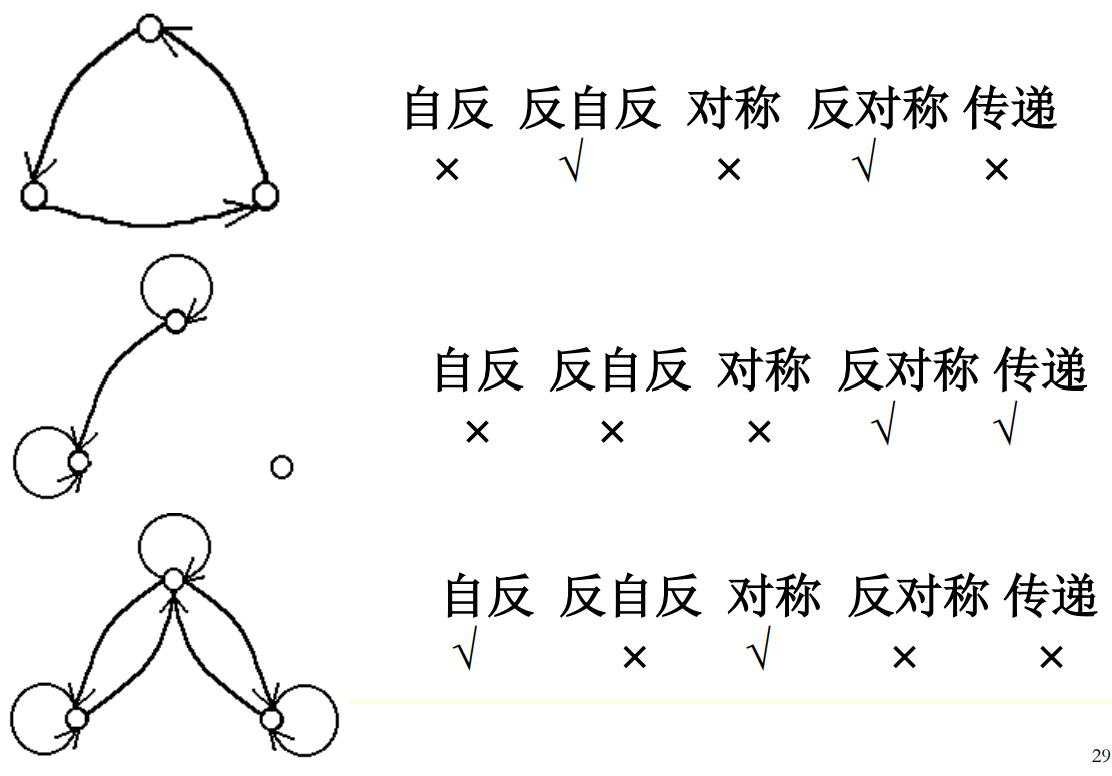
练习：考试时一般会给出A和关系R，让你判断性质。
A=[1,2,3,4];R=[<1,1><1,2><2,1><2,3><4,4>]

复合关系、逆关系

复合关系

定义复合关系：
设R是A到B的关系，S是B到C的关系，则RS称为R和S的复合关系，表示为
R°S = [<x,z> | x∈A∧z∈C∧(存在y)(y∈B∧<x,y>∈R∧<y,z>∈S)]

复合关系的性质

复合关系的关系矩阵：
由两个关系矩阵的逻辑乘（用0、1表示零和非零值）得到。
复合关系的关系图：
两点间有一点，接通这两点，省去中间点集，得到复合关系的关系图。
复合关系是不可交换的（没有公共域）
复合关系是可结合的。

逆关系

定义逆关系：
设R是A到B的关系， 将R中每一序偶元素顺序互换，得到的集合称为关系R的逆关系，表示为 Rc = { <y,x>|<x,y>∈R}可见， Rc是B到A的关系。逆关系保持了关系的性质
有关定理：

证明两个关系相等，实质上是证明两个集合（元素是序偶）相等
        (R1∪R2)c = R1c∪R2c 
        (R1∩R2)c = R1c∩R2c
        (R1-R2)c = R1c-R2c
        (AB)c = BA
        ( R1R2)c = R2c R1c
        (R1R2) R3 = R1 (R2 R3)  
R是非空集合X上的关系，有：
        R是对称的 <=> R= Rc
        R是反对称的 <=> R∩Rc 是Ix 的子集

闭包、集合的划分、集合的覆盖

关系R的自反（对称、传递）闭包：
是指包含R的、而且是自反的、最小的自反（对称、传递）关系，如果R本身是自反的（对称的、传递的），则其自反的（对称的、传递的）闭包就是R ，在原本的基础上令关系自反(对称、传递)


最大最小划分：
最小划分（划分的个数最少）：
该集合的全部元素组成一个分块。
最大划分（划分的个数最多）：
每个元素构成一个分块。
交叉划分、加细划分不要求

等价关系、等价类、偏序关系

等价关系

同时包含自反性，对称性，传递性的就是等价关系

等价类(p131)

R是A上的等价关系，则
等价类 [a]R= 【x|x∈A且aRx】
等价关系与划分互相决定，a上的等价类问由多少种等价关系，即问有多少种划分
练习：
证明<a,b>∈R<=>[a]_r=[b]_r;(主要利用对称性和传递性)