大学物理(上)
大学物理(上)
绪论
大学物理的研究内容:
力学、电磁学、热学、震动和波动、量子物理
本学期学习的内容:
第一章:质点运动学
第二章:质点动力学
第三章:刚体力学
第四章:连续体力学(自学)
第五章:机械振动
第六章:机械波
第七章:光的干涉
第八章:光的衍射
第九章:光的偏振
第十章:几何光学(自学)
质点系
第一节 参考系、坐标系、质点
坐标系:直角坐标系、极坐标系、自然坐标系等
第二节 指点位置的描述
位置矢量:r=xi+yj+zk 大小为|r| 方向余弦值:坐标/模长;
平均速度v=Δr/Δt(这个v带→和—);瞬时速度v=lim(t→0)Δr/Δt=dr/dt(这个v只带→);
平均速率v=Δs/Δt(这个v带—);瞬时速度v=lim(t→0)Δs/Δt=ds/dt(这个v什么也不带);

练习题

答案:ABCD ——–>我靠,谁家好人出题出全选的啊
第三节 切向加速度和法向加速度
一般研究这个东西的时候建立的是自由坐标系
1 | |
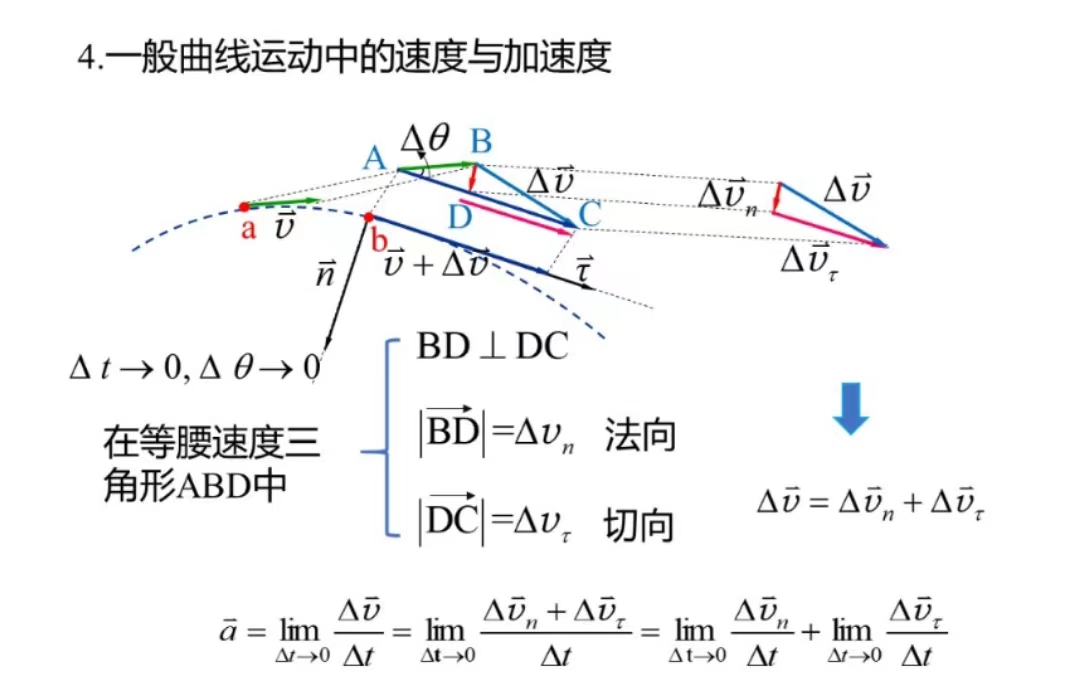
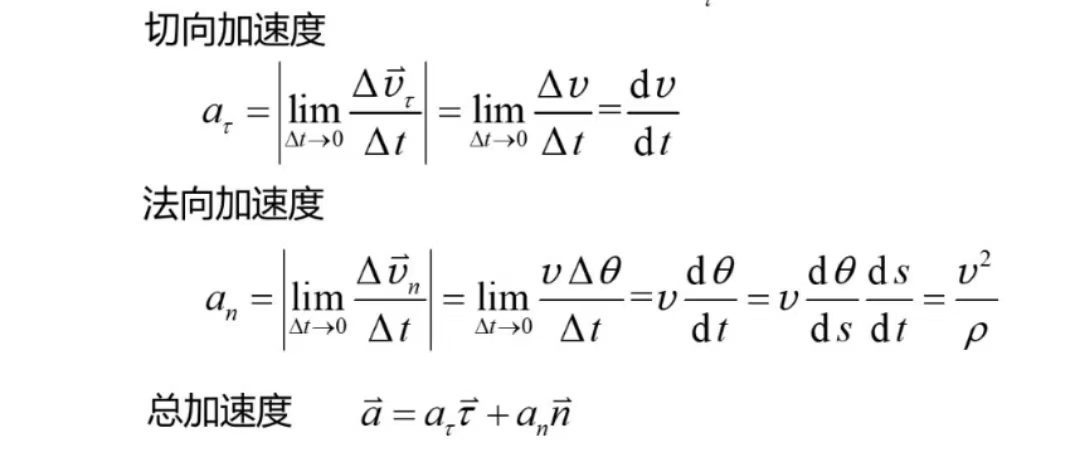
1 | |
第四节 几种常见的质点运动
平抛运动
例题:
抛体运动是典型的平面匀加速运动,已知ā=g,初速度与水平面的夹角为0,初速度大小为v,求解运动质点的运动方程、轨道方程、速度随时间的变化关系和位矢随时间的变化关系。
圆周运动
一般建立极坐标系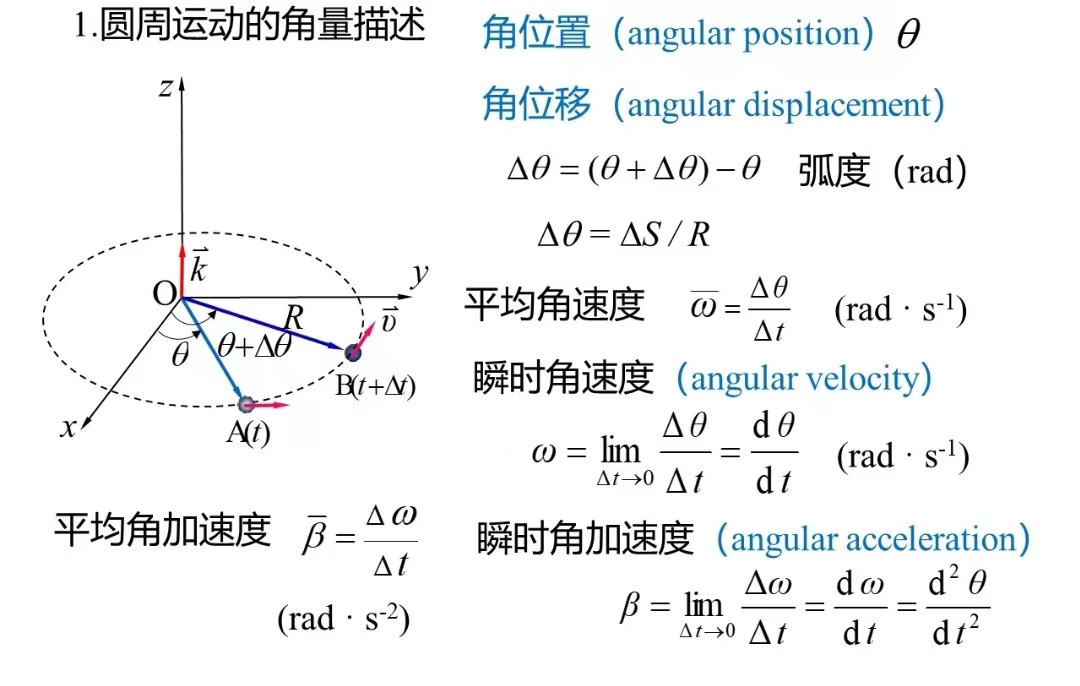
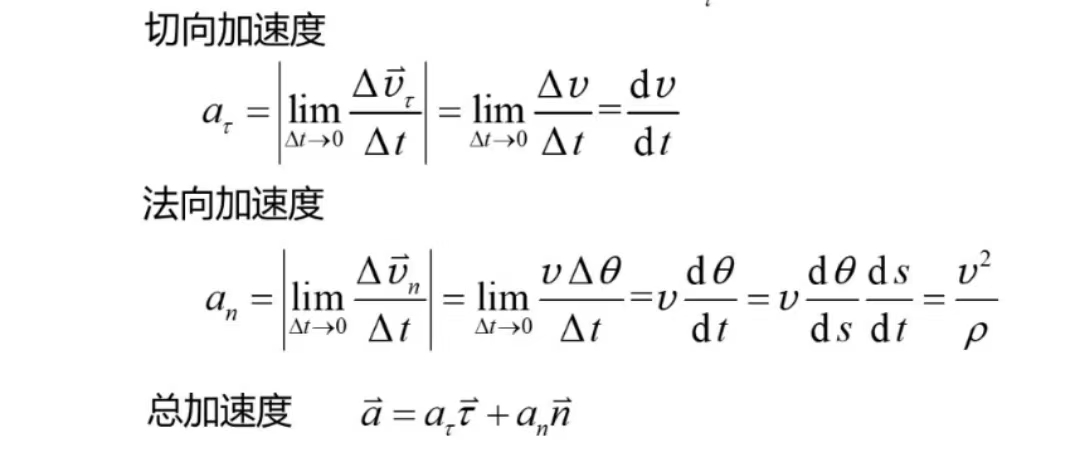
第五节 相对运动
分解成沿x、y、z方向的向量并且进行运算,同向减,异向加
第一章公式总结

质点动力学
第一节 牛顿运动定律
1 | |

1 | |
几种常见的力:
万有引力和重力(略)
弹力:(形变力)
1.正压力或支持力
2.拉力和张力(前者是外力,后者是内力)
3.弹簧的弹力
例题:关于张力的计算(注意,题目若未提及忽略绳子质量,则需要进行计算)
质量均匀分布的粗绳拉重物,已知:F=150N, a=0.2m/s2,l=4m,粗绳的质量为m=2kg.求:距顶端为 x米处绳中的张力。
例题:牛顿第二定律的应用(注意一下:第一题乘ds那一步比较重要)
1 | |
第二节 动量与动量守恒定律
冲量
n个指点组成的力学系统所受合外力的冲量等于系统总动量的增量。
内力不能改变系统的总动量(因为总是成对出现,会抵消掉);但是内力能改变每一个质点的动量。
动量定理:
质点系的动量定理: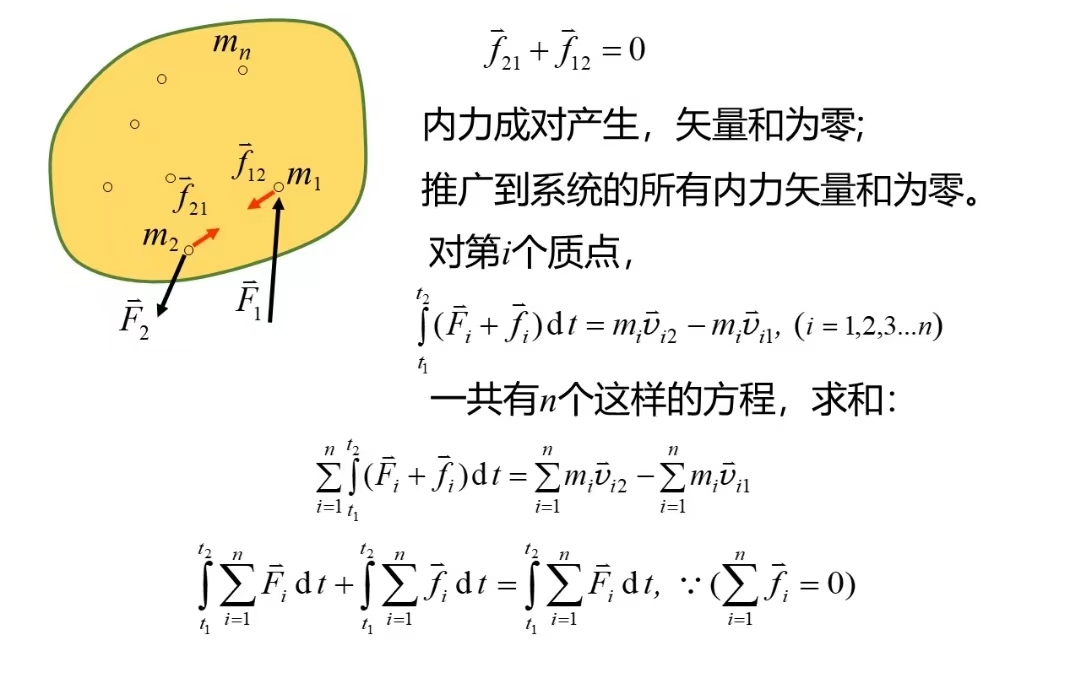
动量守恒定律
合外力为0
有三点要注意:
1 | |
练习:

一个质量m=140g的垒球以v=40m·s’的速率沿水平方向飞向击球手,被球棒击中后它以相同的速率沿着与水平方向成0=60°的仰角飞出。求垒球的平均打击力。设棒和球的接触时间为1.2ms。
变质物体的运动方程
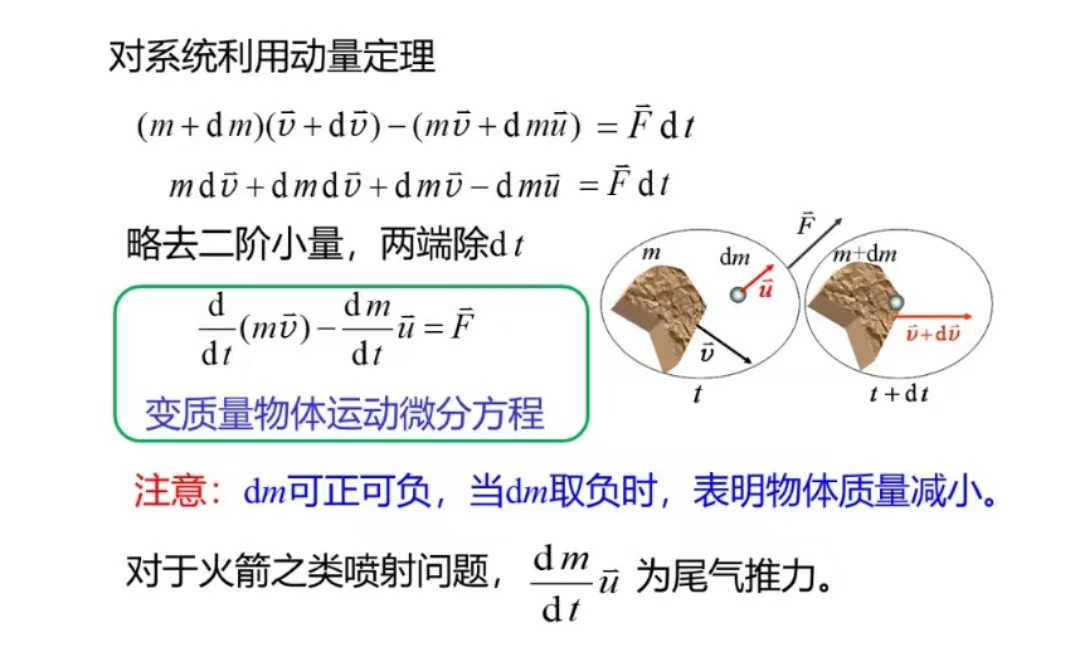
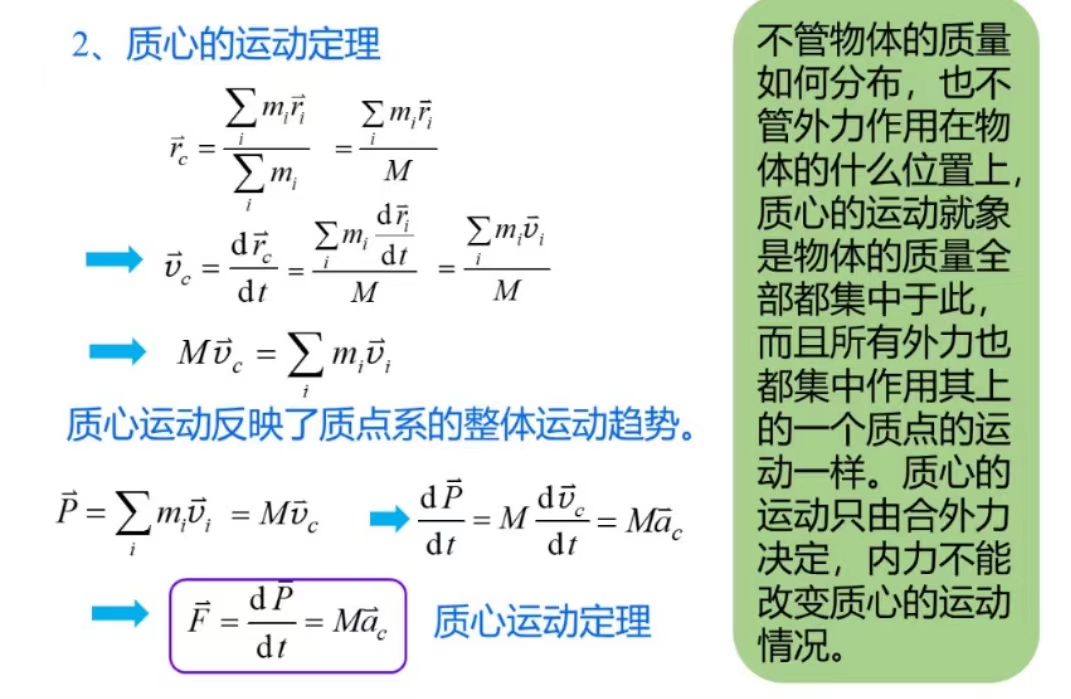
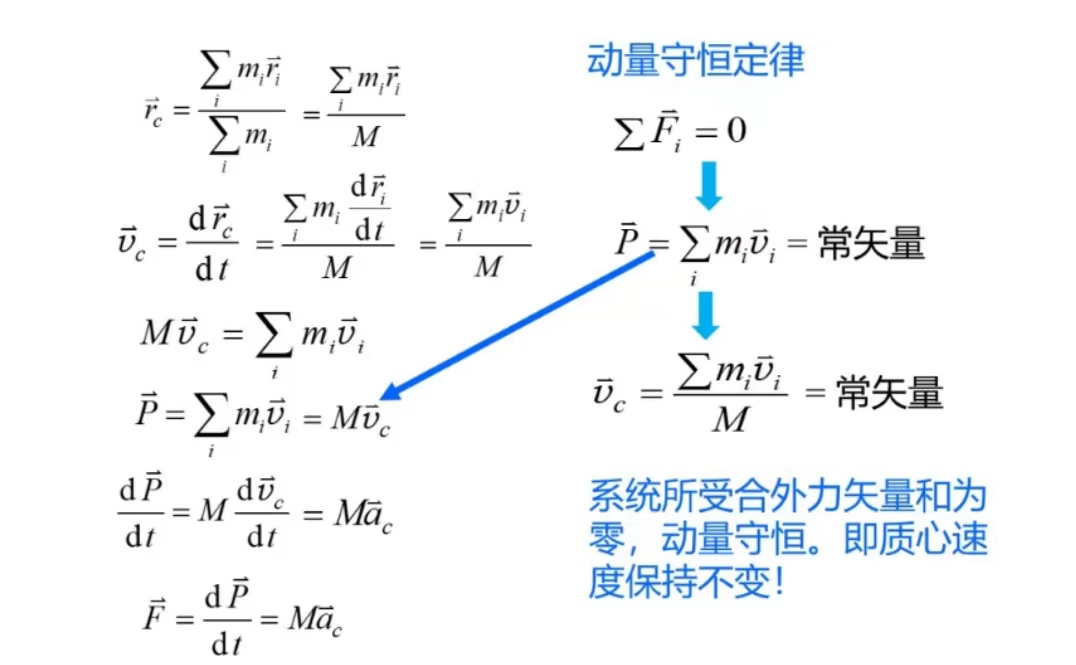
质心运动定律
质心:质点系的运动中心,质心运动反映了质点系的整体运动趋势。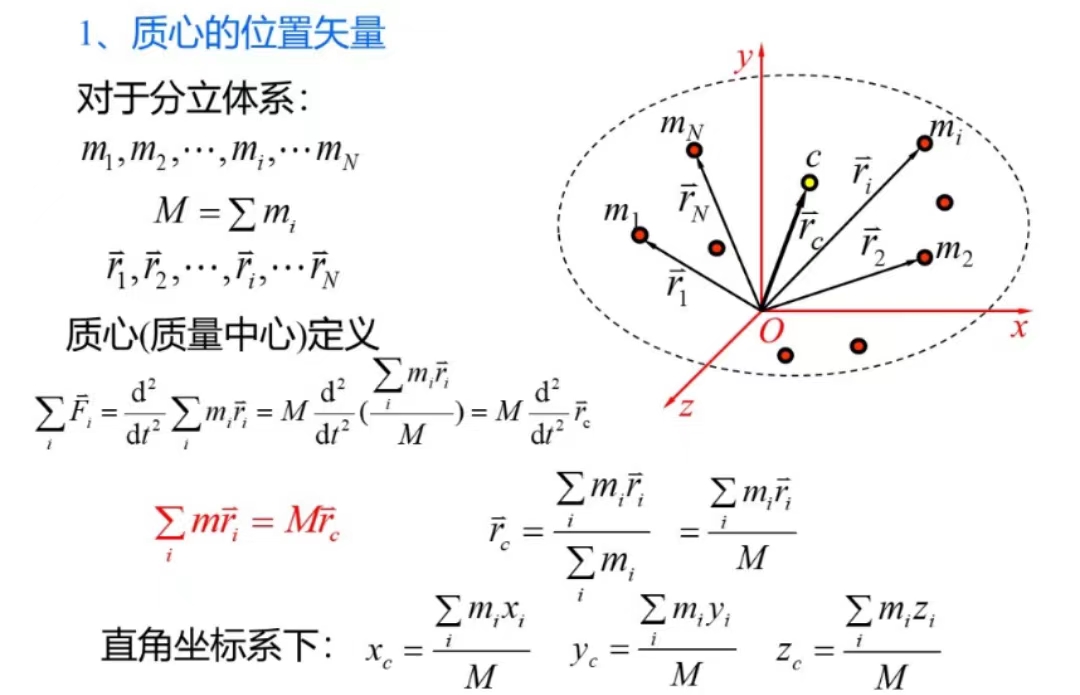
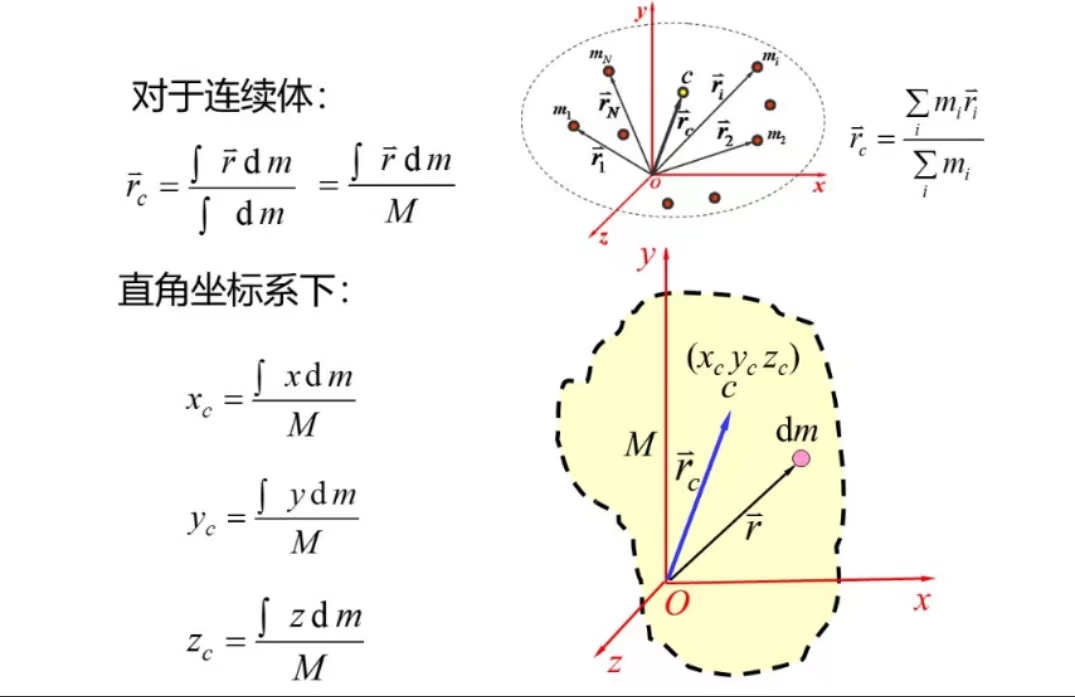
第三节 功和能
功
力在位移方向的积累
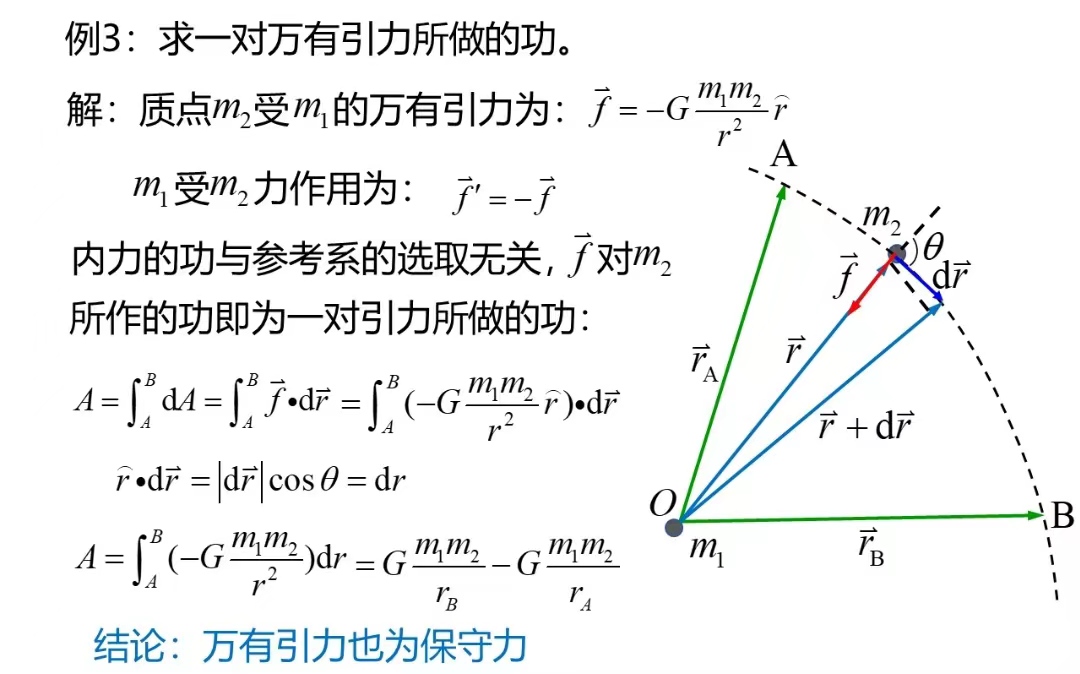
保守力和非保守力:力做的功是否与过程和路径有关
观察一下计算的方法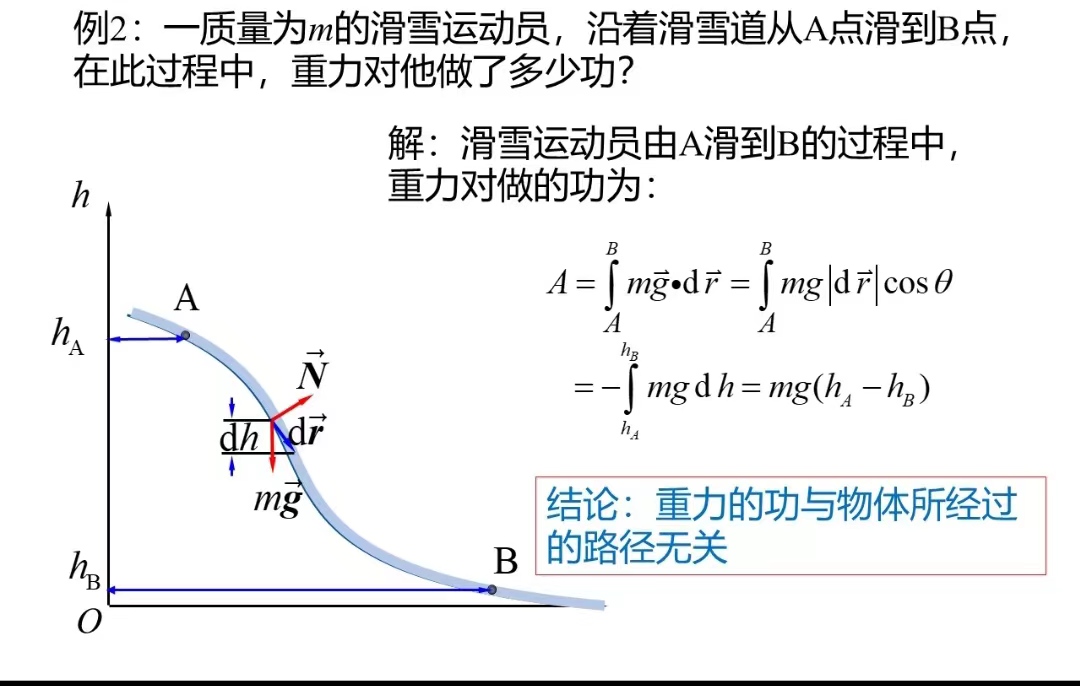
功率

动能定理
质点的动能定理
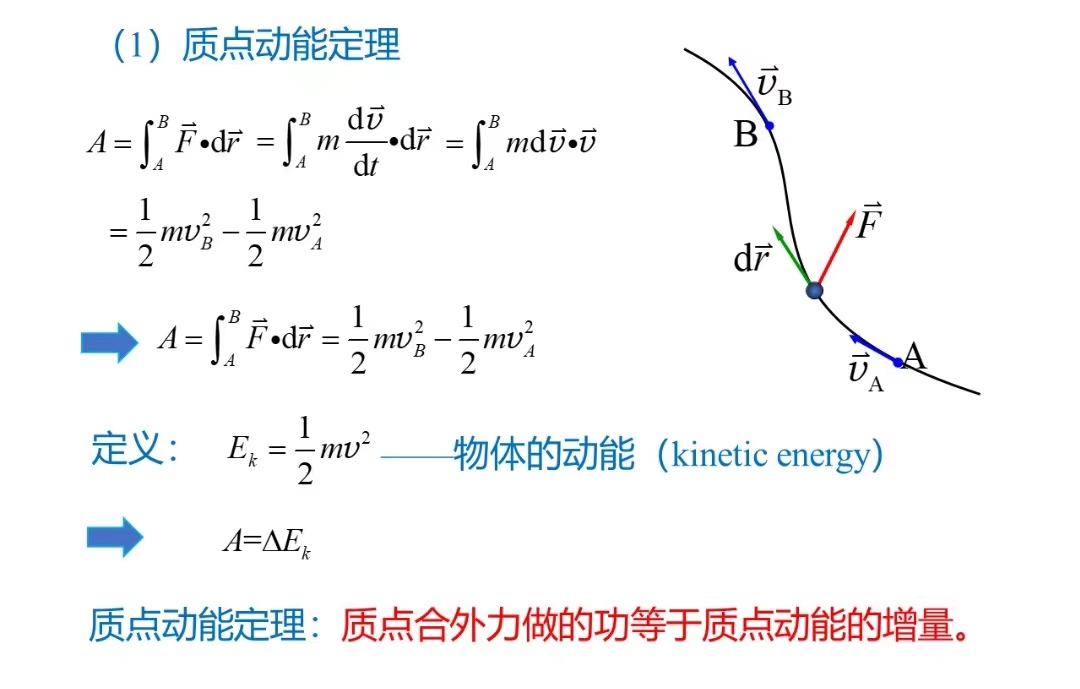
质点系的动能定理

势能

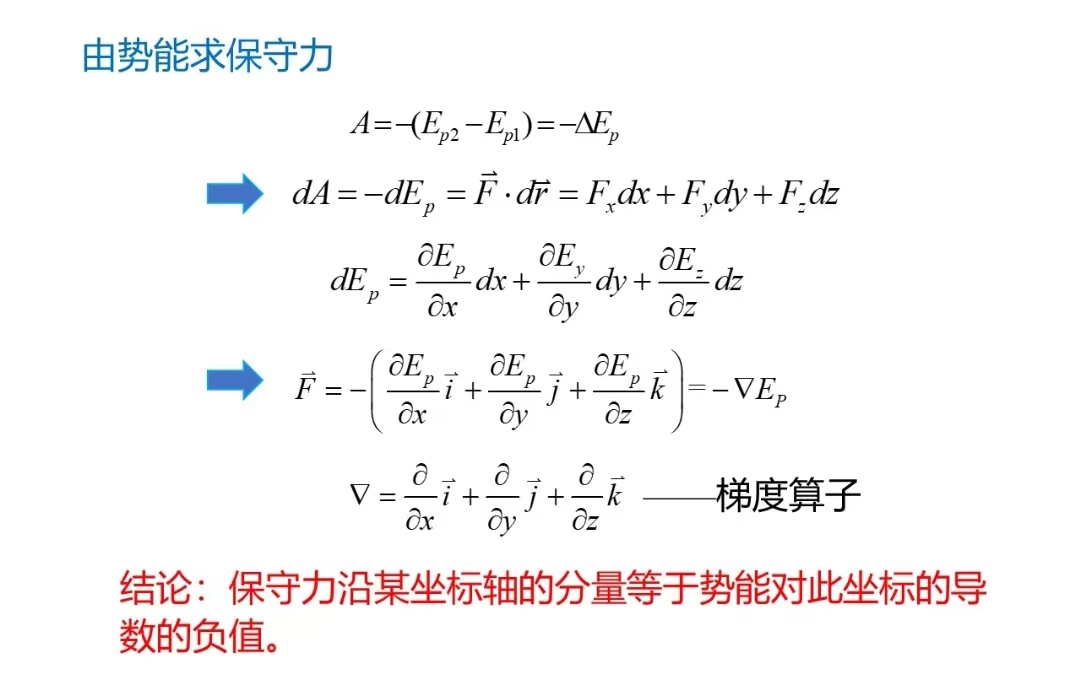
功能原理和机械能守恒定律
1 | |
例题
1 | |
第四节 角动量 角动量守恒定律
角动量(又叫动量矩)L=r×P=|r|*|P|*sinα=Iw=mvr; (方向用右手螺旋定则判断)
力矩:M=r×F=|r|*|F|*sinα
角动量定理
M=dL/dt;力矩在某方向上的分量Mz=dLz/dt;
角动量守恒定律
M=0时,L=常矢量;
例题: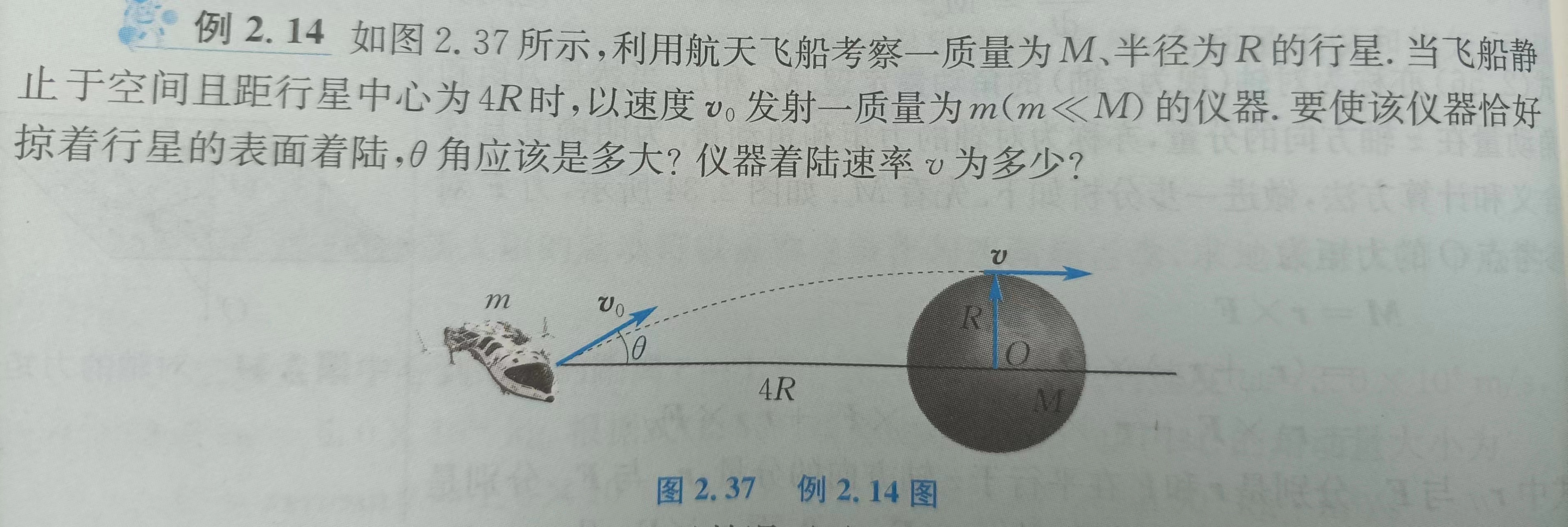
第二章公式小结

刚体力学
刚体运动学
刚体:任意两质点之间的距离在外里作用下始终保持不变的物体
平动:沿着一条直线运动,可以看成是质点
转动
转动的角速度、定轴转动等,看第一章就行
例题: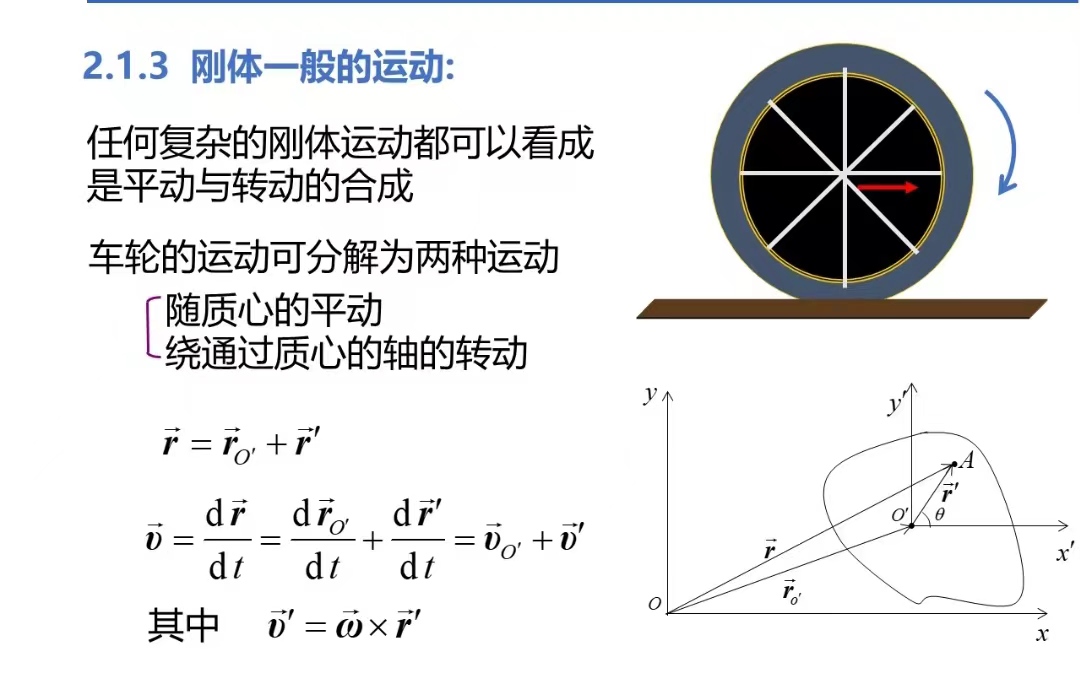

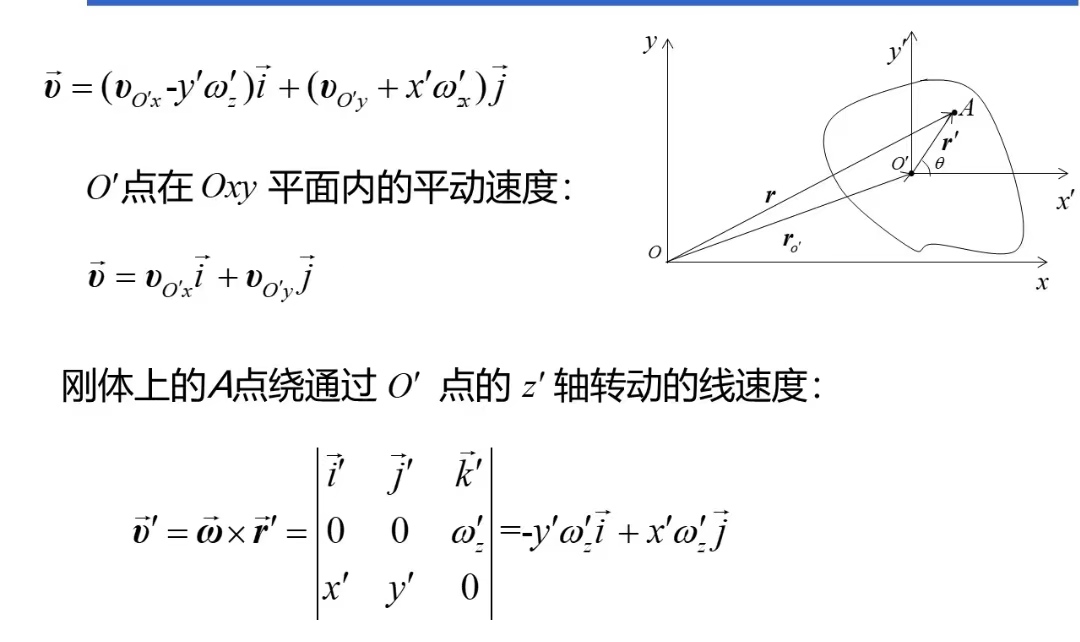
刚体动力学
M=r×F(这里的F指的是外力在转动平面的分力)
注意:
1 | |
例题:
1 | |
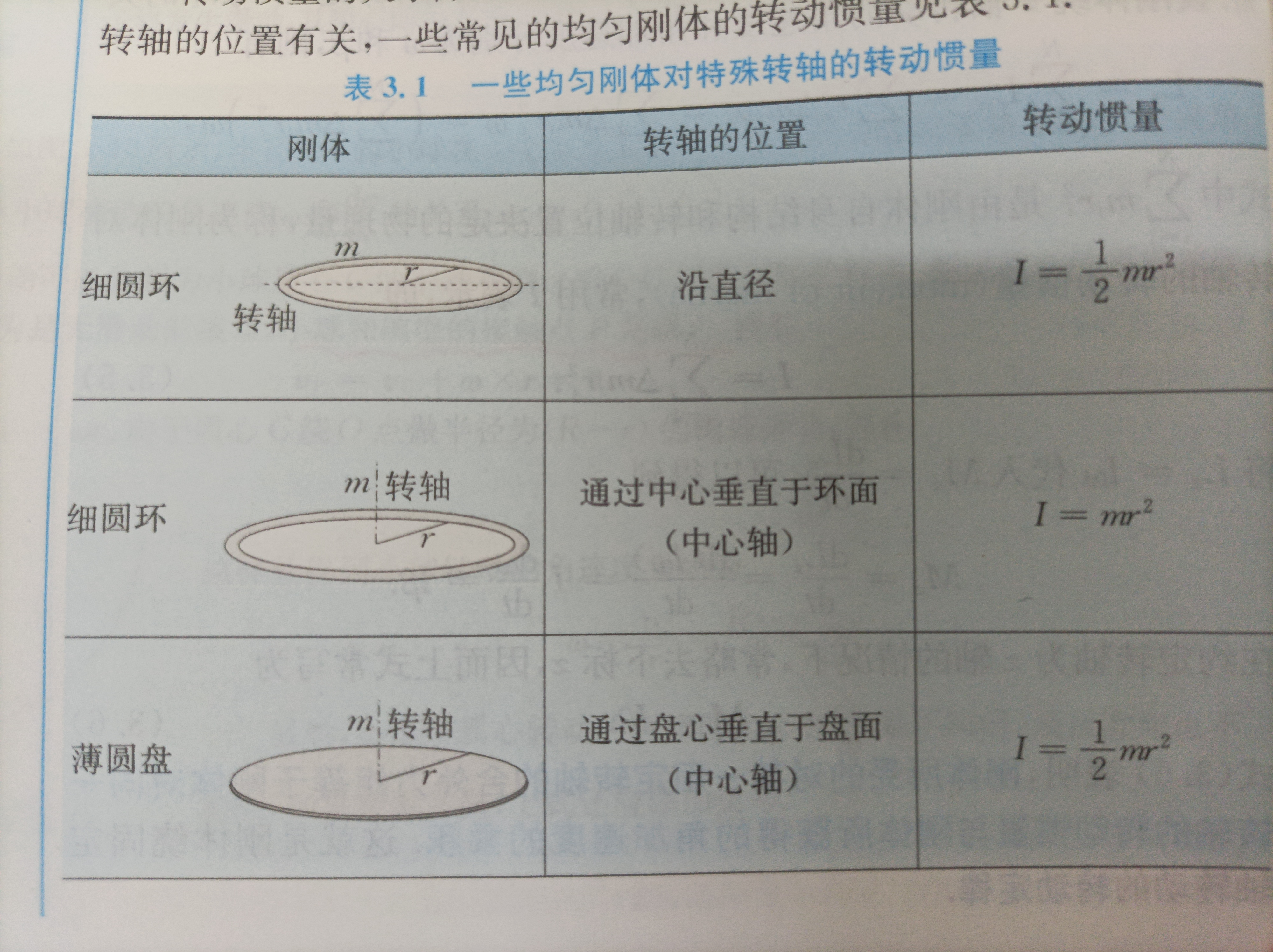
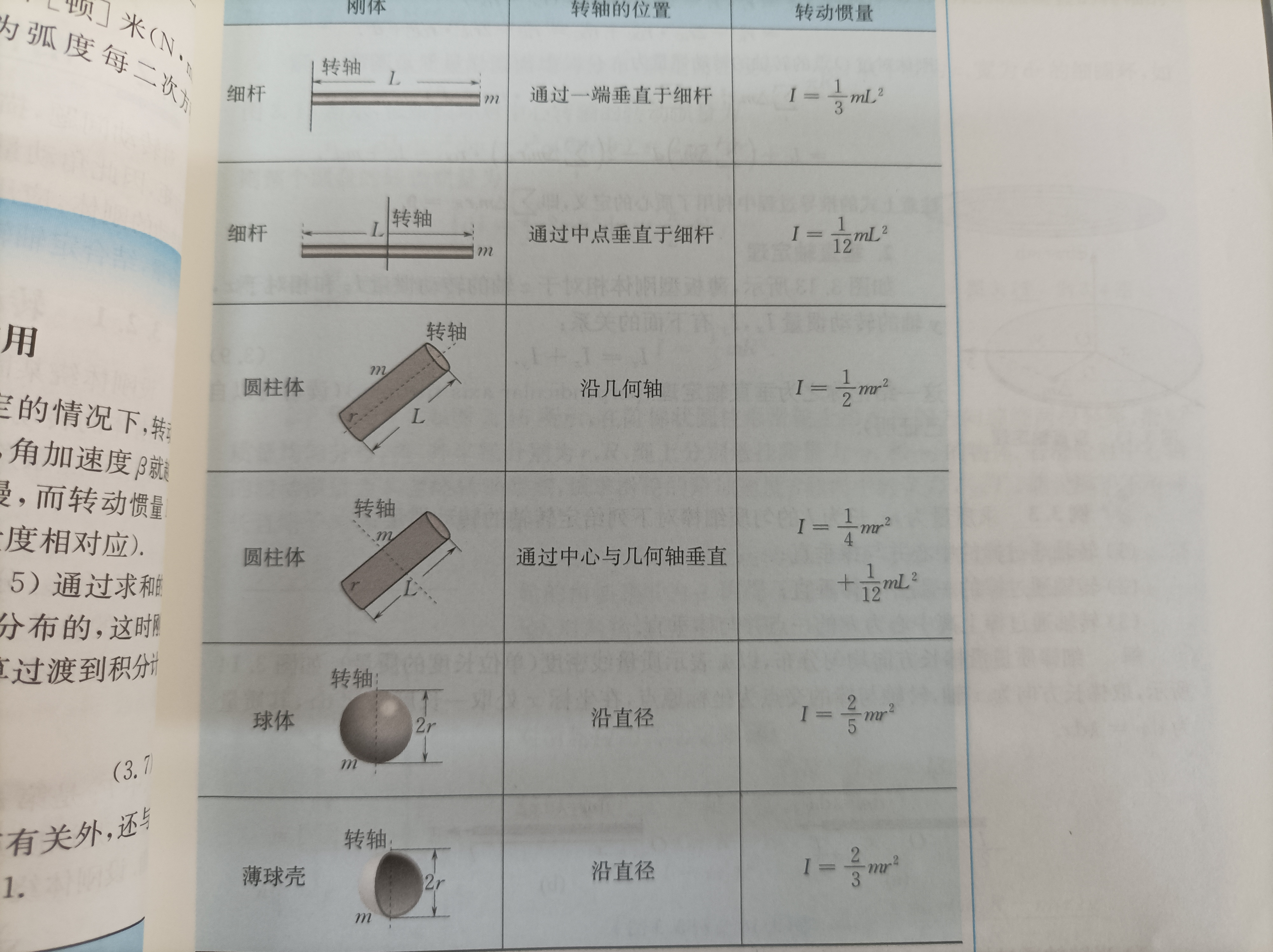
刚体的转动惯量:


平行轴定理和垂直轴定理(注意一下平行轴定理是比较重要的内容)

三个例题,区分一下:
1 | |
冲量矩和角动量守恒定律
角动量守恒:
1 | |
力矩的功
表达方式:力矩M在θ上的积累
动能:1/2Iw^2-1/2Iw^2(相关量的记忆方法:把I当成m,M当成F)
第三章必须要记得的结论
振动力学
简谐振动的描述
振动时一种特殊的运动形式。有特定值和周期性。(在某一特定值附近来回变化,具有周期性)
简谐振动:运动时物体的位移(或角位移)和时间的函数图象为正余弦函数。
1 | |
1 | |
当给出沿x轴正方向运动时—>表示v>0
简谐运动的动力学方程
平衡位置
1 | |
回复力
回复力(力矩):
使物体回到平衡位置的力(力矩)。常见的力为:弹力、分子间作用力、重力等;
合外力和位移始终反向,且合外力的方向始终指向平衡位置。
线性回复力(F与位移成正比,与位移方向相反)
F=-kx–>d^2x/dt^2+w^2x=0(w=(k/m)^1/2)
弹簧谐振子w:固有(圆)频率(☆取决于系统内在性质)
位移通解x:Acos(wt+φ)
水平弹簧振子
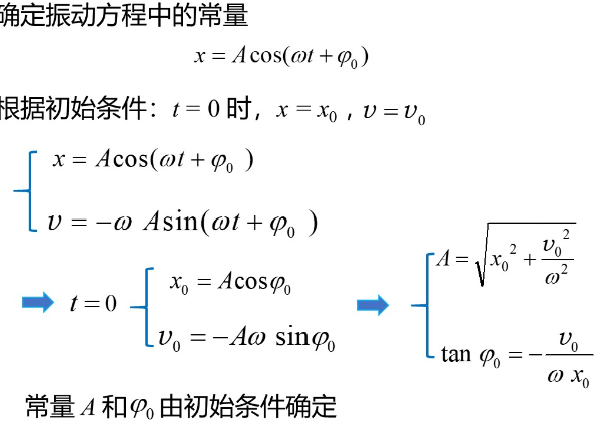
竖直弹簧振子
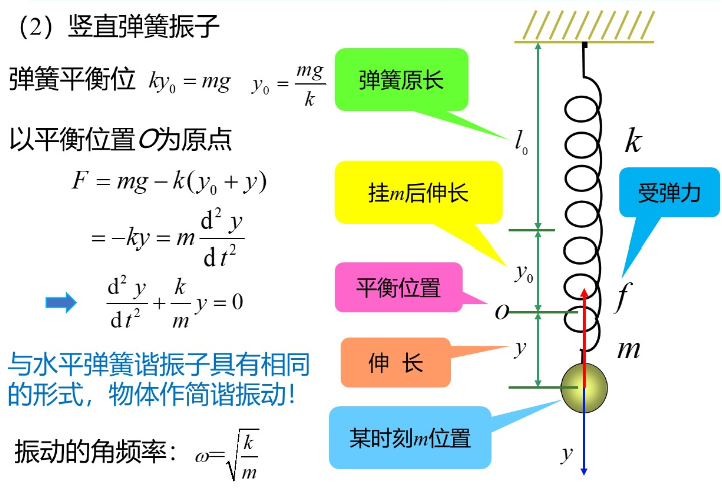
单摆
T=2PI(l/g)^1/2
复摆
下面这个例题用了平行轴定理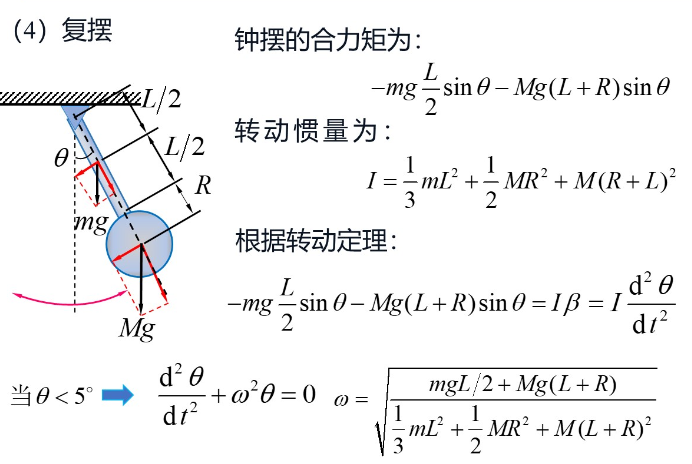
简谐振动的能量
水平弹簧振子的能量
E_k=1/2mw^2A^2sin^2(wt+φ);
E_p=1/2kA^2cos^2(wt+φ);
k=w^2m;
一个周期内动能和势能的平均值为1/4 kA^2;
简谐运动的合成
解析法或图像法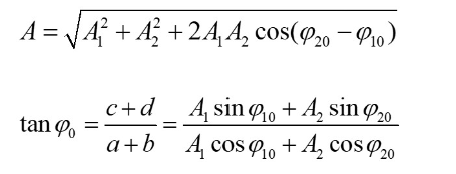
例题:
求N个同方向、同频率的简谐振动的和振动。